Introduction of Lines And Angles Notes
Parallel lines with a transversal
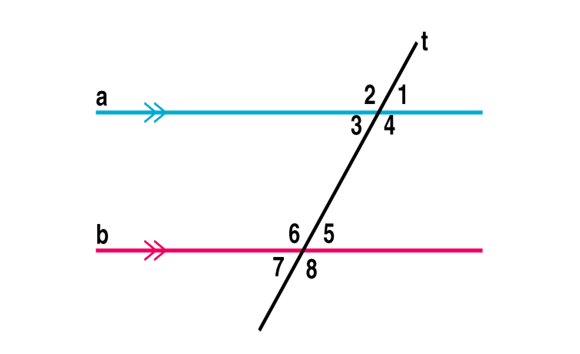
- ∠1=∠5,∠2=∠6,∠4=∠8 and ∠3=∠7(Corresponding angles)
- ∠3=∠5,∠4=∠6 (Alternate interior angles)
- ∠1=∠7,∠2=∠8 (Alternate exterior angles)
Lines parallel to the same line
Lines that are parallel to the same line are also parallel to each other.
Introduction to Geometry
Angles and types of angles
When 2 rays originate from the same point at different directions, they form an angle.
– The rays are called arms and the common point is called the vertex
– Types of angles : (i) Acute angle 0∘<a<90∘
(ii) Right angle a=90∘
(iii) Obtuse angle : 90∘<a<180∘
(iv) Straight angle =180∘
(v) Reflex Angle 180∘<a<360∘
(vi) Angles that add up to 90∘ are complementary angles
(vii) Angles that add up to 180∘ are called supplementary angles.
Intersecting Lines and Associated Angles
Intersecting and Non-Intersecting lines
- When 2 lines meet at a point they are called intersecting
- When 2 lines never meet at a point, they are called non-intersecting or parallel lines
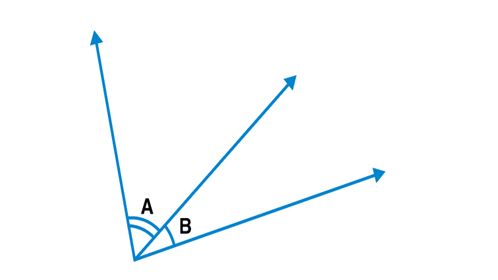
Adjacent angles
2 angles are adjacent if they have the same vertex and one common point.
Linear Pair
When 2 adjacent angles are supplementary, i.e they form a straight line (add up to 180∘), they are called a linear pair.
Vertically opposite angles
When two lines intersect at a point, they form equal angles that are vertically opposite to each other.
Basic Properties of a Triangle
Triangle and sum of its internal angles
Sum of all angles of a triangle add up to 180∘
An exterior angle of a triangle = sum of opposite internal angles
– If a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles

– ∠4=∠1+∠2