Exercise: 6.2 (Page No: 103)
1. In Fig. 6.28, find the values of x and y and then show that AB CD.
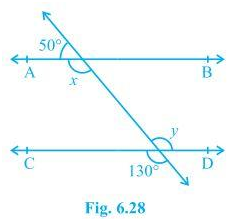
Solution:
We know that a linear pair is equal to 180°.
So, x+50° = 180°
∴ x = 130°
We also know that vertically opposite angles are equal.
So, y = 130°
In two parallel lines, the alternate interior angles are equal. In this,
x = y = 130°
This proves that alternate interior angles are equal and so, AB CD.
2. In Fig. 6.29, if AB CD, CD EF and y : z = 3 : 7, find x.

Solution:
It is known that AB CD and CDEF
As the angles on the same side of a transversal line sums up to 180°,
x + y = 180° —–(i)
Also,
O = z (Since they are corresponding angles)
and, y +O = 180° (Since they are a linear pair)
So, y+z = 180°
Now, let y = 3w and hence, z = 7w (As y : z = 3 : 7)
∴ 3w+7w = 180°
Or, 10 w = 180°
So, w = 18°
Now, y = 3×18° = 54°
and, z = 7×18° = 126°
Now, angle x can be calculated from equation (i)
x+y = 180°
Or, x+54° = 180°
∴ x = 126°
3. In Fig. 6.30, if AB CD, EF ⊥ CD and GED = 126°, find AGE, GEF and FGE.
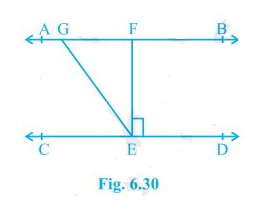
Solution:
Since AB CD, GE is a transversal.
It is given that GED = 126°
So, GED = AGE = 126° (As they are alternate interior angles)
Also,
GED = GEF +FED
As EF⊥ CD, FED = 90°
∴ GED = GEF+90°
Or, GEF = 126° – 90° = 36°
Again, FGE +GED = 180° (Transversal)
Putting the value of GED = 126° we get,
FGE = 54°
So,
AGE = 126°
GEF = 36° and
FGE = 54°
4. In Fig. 6.31, if PQ ST, PQR = 110° and RST = 130°, find QRS.
[Hint : Draw a line parallel to ST through point R.]
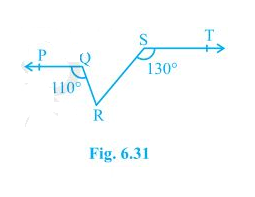
Solution:
First, construct a line XY parallel to PQ.

We know that the angles on the same side of transversal is equal to 180°.
So, PQR+QRX = 180°
Or,QRX = 180°-110°
∴ QRX = 70°
Similarly,
RST +SRY = 180°
Or, SRY = 180°- 130°
∴ SRY = 50°
Now, for the linear pairs on the line XY-
QRX+QRS+SRY = 180°
Putting their respective values, we get,
QRS = 180° – 70° – 50°
Hence, QRS = 60°
5. In Fig. 6.32, if AB CD, APQ = 50° and PRD = 127°, find x and y.
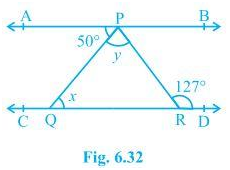
Solution:
From the diagram,
APQ = PQR (Alternate interior angles)
Now, putting the value of APQ = 50° and PQR = x we get,
x = 50°
Also,
APR = PRD (Alternate interior angles)
Or, APR = 127° (As it is given that PRD = 127°)
We know that
APR = APQ+QPR
Now, putting values of QPR = y and APR = 127° we get,
127° = 50°+ y
Or, y = 77°
Thus, the values of x and y are calculated as:
x = 50° and y = 77°
6. In Fig. 6.33, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB CD.

Solution:
First, draw two lines BE and CF such that BE ⊥ PQ and CF ⊥ RS.
Now, since PQ RS,
So, BE CF

We know that,
Angle of incidence = Angle of reflection (By the law of reflection)
So,
1 = 2 and
3 = 4
We also know that alternate interior angles are equal. Here, BE ⊥ CF and the transversal line BC cuts them at B and C
So, 2 = 3 (As they are alternate interior angles)
Now, 1 +2 = 3 +4
Or, ABC = DCB
So, AB CD alternate interior angles are equal)