Introduction to Circles
Circles
- The set of all the points in a plane that is at a fixed distance from a fixed point makes a circle.
- A Fixed point from which the set of points are at fixed distance is called the centre of the circle.
- A circle divides the plane into 3 parts: interior (inside the circle), the circle itself and exterior (outside the circle)
Radius
– The distance between the centre of the circle and any point on its edge is called the radius.
Tangent and Secant
A line that touches the circle at exactly one point is called it’s tangent. A line that cuts a circle at two points is called a secant.

In the above figure: PQ is the tangent and AB is the secant.
Chord
-The line segment within the circle joining any 2 points on the circle is called the chord.
Diameter
– A Chord passing through the centre of the circle is called the diameter. – The Diameter is 2 times the radius and it is the longest chord.
Arc
– The portion of a circle(curve) between 2 points is called an arc. – Among the two pieces made by an arc, the longer one is called a major arc and the shorter one is called a minor arc.
Circumference
The perimeter of a circle is the distance covered by going around its boundary once. The perimeter of a circle has a special name: Circumference, which is π times the diameter which is given by the formula 2πr
Segment and Sector
– A circular segment is a region of a circle which is “cut off” from the rest of the circle by a secant or a chord. – Smaller region cut off by a chord is called minor segment and the bigger region is called major segment. –
-A sector is the portion of a circle enclosed by two radii and an arc, where the smaller area is known as the minor sector and the larger being the major sector.
– For 2 equal arcs or for semicircles – both the segment and sector is called the semicircular region.
Circles and Their Chords
Theorem of equal chords subtending angles at the centre.
– Equal chords subtend equal angles at the centre.

Proof: AB and CD are the 2 equal chords.
In Δ AOB and Δ COD
OB = OC [Radii]
OA = OD [Radii]
AB = CD [Given]
ΔAOB ≅ ΔCOD (SSS rule)
Hence, ∠AOB = ∠COD [CPCT]
Theorem of equal angles subtended by different chords.
– If the angles subtended by the chords of a circle at the centre are equal, then the chords are equal.
Proof: In ΔAOB and ΔCOD
OB = OC [Radii] ∠AOB=∠COD [Given]
OA = OD [Radii]
ΔAOB ≅ ΔCOD (SAS rule)
Hence, AB=CD [CPCT]
Perpendicular from the centre to a chord bisects the chord.
Perpendicular from the centre of a circle to a chord bisects the chord.

Proof: AB is a chord and OM is the perpendicular drawn from the centre.
From ΔOMB and ΔOMA,
∠OMA=∠OMB=900 OA = OB (radii)
OM = OM (common)
Hence, ΔOMB ≅ ΔOMA (RHS rule)
Therefore AM = MB [CPCT]
A Line through the centre that bisects the chord is perpendicular to the chord.
– A line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.
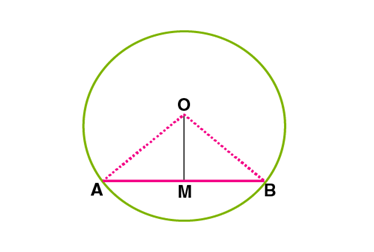
Proof: OM drawn from the center to bisect chord AB.
From ΔOMA and ΔOMB,
OA = OB (Radii)
OM = OM (common)
AM = BM (Given)
Therefore, ΔOMA ≅ ΔOMB (SSS rule)
⇒∠OMA=∠OMB (C.P.C.T)
But, ∠OMA+∠OMB=1800
Hence, ∠OMA=∠OMB=900 ⇒OM⊥AB
Circle through 3 points
– There is one and only one circle passing through three given noncollinear points. – A unique circle passes through 3 vertices of a triangle ABC called as the circumcircle. The centre and radius are called the circumcenter and circumradius of this triangle, respectively.
Equal chords are at equal distances from the centre.
Equal chords of a circle(or of congruent circles) are equidistant from the centre (or centres).

Proof: Given, AB = CD, O is the centre. Join OA and OC.
Draw, OP⊥AB, OQ⊥CD
In ΔOAP and ΔOCQ,
OA=OC (Radii)
AP=CQ ( AB = CD ⇒(1/2)AB = (1/2)CD since OP and OQ bisects the chords AB and CD.)
ΔOAP ≅ ΔOCQ (RHS rule)
Hence, OP=OQ (C.P.C.T.C)
Chords equidistant from the centre are equal
Chords equidistant from the centre of a circle are equal in length.

Proof: Given OX = OY (The chords AB and CD are at equidistant) OX⊥AB, OY⊥CD
In ΔAOX and ΔDOY
∠OXA =∠OYD (Both 900)
OA = OD (Radii)
OX = OY (Given)
ΔAOX ≅ ΔDOY (RHS rule)
Therefore AX = DY (CPCT)
Similarly XB = YC
So, AB = CD
Circles and Quadrilaterals
The angle subtended by an arc of a circle on the circle and at the centre
The angle subtended by an arc at the centre is double the angle subtended by it on any part of the circle.
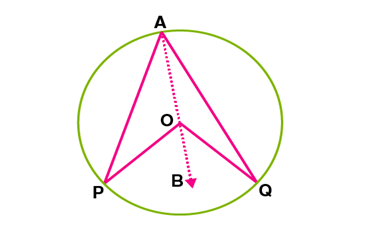
Here PQ is the arc of a circle with centre O, that subtends ∠POQ at the centre.
Join AO and extend it to B.
In ΔOAQ OA = OQ….. [Radii]
Hence, ∠OAQ = ∠OQA ……..[Property of isosceles triangle]
Implies ∠BOQ = 2∠OAQ …..[Exterior angle of triangle = Sum of 2 interior angles]
Similarly, ∠BOP = 2∠OAP
⇒∠BOQ + ∠BOP = 2∠OAQ + 2∠OAP
⇒∠POQ = 2∠PAQ
Hence proved.
Angles in the same segment of a circle.
–Angles in the same segment of a circle are equal.

Consider a circle with centre O.
∠PAQ and ∠PCQ are the angles formed in the major segment PACQ with respect to the arc PQ.
Join OP and OQ
∠POQ = 2∠PAQ = 2∠PCQ ……….[ Angle subtended by an arc at the centre is double the angle subtended by it in any part of the circle]
⇒∠PCQ = ∠PAQ
Hence proved
The angle subtended by diameter on the circle
– Angle subtended by diameter on a circle is a right angle. (Angle in a semicircle is a right angle)

Consider a circle with centre O, POQ is the diameter of the circle.
∠PAQ is the angle subtended by diameter PQ at the circumference.
∠POQ is the angle subtended by diameter PQ at the centre.
∠PAQ = (1/2)∠POQ……..[Angle subtended by arc at the centre is double the angle at any other part]
∠PAQ = (1/2) × 1800 = 900
Hence proved
Line segment that subtends equal angles at two other points
– If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment, the four points lie on a circle (i.e they are concyclic).
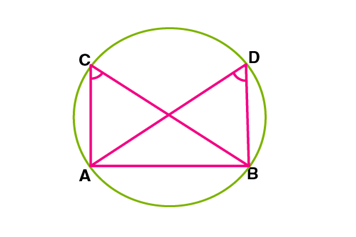
Here ∠ACB=∠ADB and all 4 points A, B, C, D are concyclic.
Cyclic Quadrilateral
– A Quadrilateral is called a cyclic quadrilateral if all the four vertices lie on a circle.

In a circle, if all four points A, B, C and D lie on the circle, then quadrilateral ABCD is a cyclic quadrilateral.
Sum of opposite angles of a cyclic quadrilateral
– If the sum of a pair of opposite angles of a quadrilateral is 180 degree, the quadrilateral is cyclic.
Sum of pair of opposite angles in a quadrilateral
– The sum of either pair of opposite angles of a cyclic quadrilateral is 180 degree.