Exercise: 6.3 (Page No: 107)
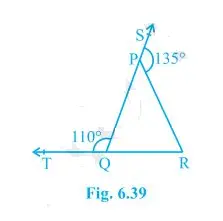
1. In Fig. 6.39, sides QP and RQ of ΔPQR are produced to points S and T respectively. If SPR = 135° and PQT = 110°, find PRQ.
Solution:
It is given the TQR is a straight line and so, the linear pairs (i.e. TQP and PQR) will add up to 180°
So, TQP +PQR = 180°
Now, putting the value of TQP = 110° we get,
PQR = 70°
Consider the ΔPQR,
Here, the side QP is extended to S and so, SPR forms the exterior angle.
Thus, SPR (SPR = 135°) is equal to the sum of interior opposite angles. (Triangle property)
Or, PQR +PRQ = 135°
Now, putting the value of PQR = 70° we get,
PRQ = 135°-70°
Hence, PRQ = 65°
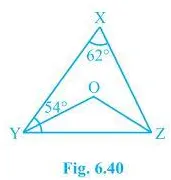
2. In Fig. 6.40, X = 62°, XYZ = 54°. If YO and ZO are the bisectors of XYZ and XZY respectively of Δ XYZ, find OZY and YOZ.
Solution:
We know that the sum of the interior angles of the triangle.
So, X +XYZ +XZY = 180°
Putting the values as given in the question we get,
62°+54° +XZY = 180°
Or, XZY = 64°
Now, we know that ZO is the bisector so,
OZY = ½ XZY
∴ OZY = 32°
Similarly, YO is a bisector and so,
OYZ = ½ XYZ
Or, OYZ = 27° (As XYZ = 54°)
Now, as the sum of the interior angles of the triangle,
OZY +OYZ +O = 180°
Putting their respective values, we get,
O = 180°-32°-27°
Hence, O = 121°
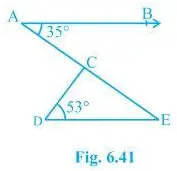
3. In Fig. 6.41, if AB DE, BAC = 35° and CDE = 53°, find DCE.
Solution:
We know that AE is a transversal since AB DE
Here BAC and AED are alternate interior angles.
Hence, BAC = AED
It is given that BAC = 35°
AED = 35°
Now consider the triangle CDE. We know that the sum of the interior angles of a triangle is 180°.
∴ DCE+CED+CDE = 180°
Putting the values, we get
DCE+35°+53° = 180°
Hence, DCE = 92°
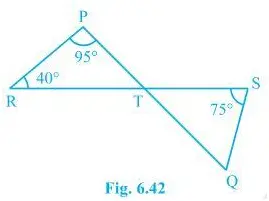
4. In Fig. 6.42, if lines PQ and RS intersect at point T, such that PRT = 40°, RPT = 95° and TSQ = 75°, find SQT.
Solution:
Consider triangle PRT.
PRT +RPT + PTR = 180°
So, PTR = 45°
Now PTR will be equal to STQ as they are vertically opposite angles.
So, PTR = STQ = 45°
Again, in triangle STQ,
TSQ +PTR + SQT = 180°
Solving this we get,
SQT = 60°
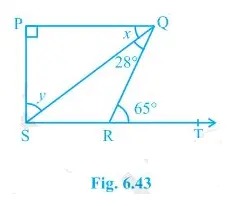
5. In Fig. 6.43, if PQ ⊥ PS, PQ SR, SQR = 28° and QRT = 65°, then find the values of x and y.
Solution:
x +SQR = QRT (As they are alternate angles since QR is transversal)
So, x+28° = 65°
∴ x = 37°
It is also known that alternate interior angles are same and so,
QSR = x = 37°
Also, Now,
QRS +QRT = 180° (As they are a Linear pair)
Or, QRS+65° = 180°
So, QRS = 115°
Now, we know that the sum of the angles in a quadrilateral is 360°. So,
P +Q+R+S = 360°
Putting their respective values, we get,
S = 360°-90°-65°-115°
Or, QS +y = 360°
y = 360°-90°-65°-115° -37°
Hence, y = 53°
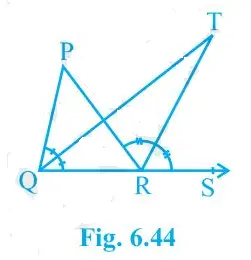
6. In Fig. 6.44, the side QR of ΔPQR is produced to a point S. If the bisectors of PQR and PRS meet at point T, then prove that QTR = ½ QPR.
Solution:
Consider the ΔPQR. PRS is the exterior angle and QPR and PQR are interior angles.
So, PRS = QPR+PQR (According to triangle property)
Or, PRS -PQR = QPR ———–(i)
Now, consider the ΔQRT,
TRS = TQR+QTR
Or, QTR = TRS-TQR
We know that QT and RT bisect PQR and PRS respectively.
So, PRS = 2 TRS and PQR = 2TQR
Now, QTR = ½ PRS – ½PQR
Or, QTR = ½ (PRS -PQR)
From (i) we know that PRS -PQR = QPR
So, QTR = ½ QPR (hence proved).