Important Questions & Solutions For Class 9 Maths Chapter 11 (Constructions)
Q.1: Construct an equilateral triangle, given its side and justify the construction.
Solution:
Construction Procedure:
- Let draw a line segment AB=4 cm .
- With A and B as centres, draw two arcs on the line segment AB and note the point as D and E.
- With D and E as centres, draw the arcs that intersect the previous arc respectively that forms an angle of 60° each.
- Now, draw the lines from A and B that are extended to meet each other at point C.
- Therefore, ABC is the required triangle.

Justification:
From construction, it is observed that
AB = 4 cm, ∠A = 60° and ∠B = 60°
We know that, the sum of the interior angles of a triangle is equal to 180°
∠A + ∠B + ∠C = 180°
SuBstitute the values
⇒ 60° + 60° + ∠C = 180°
⇒ 120° + ∠C = 180°
⇒ ∠C = 60°
While measuring the sides, we get
BC = CA = 4 cm (Sides opposite to equal angles are equal)
AB = BC = CA = 4 cm
∠A = ∠B = ∠C = 60°
Hence, justified.
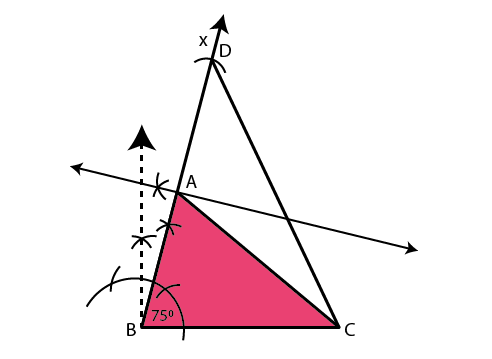
Q.2: Construct a triangle ABC in which BC = 7cm, ∠B = 75° and AB + AC = 13 cm.
Solution:
Construction Procedure:
The steps to draw the triangle of given measurement is as follows:
- Draw a line segment of base BC = 7 cm
- Measure and draw ∠B = 75° and draw the ray BX
- Take a compass and measure AB + AC = 13 cm.
- With B as a centre and draw an arc at the point be D
- Join DC
- Now draw the perpendicular bisector of the line BD and the intersection point is taken as A.
- Now join AC
- Therefore, ABC is the required triangle.
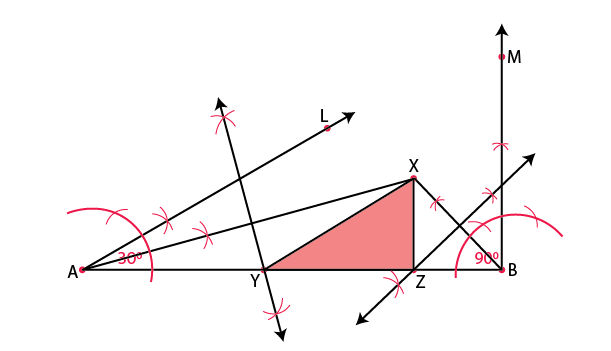
Q.3: Construct a triangle XYZ in which ∠Y = 30°, ∠Z = 90° and XY + YZ + ZX = 11 cm.
Solution:
Construction Procedure:
The steps to draw the triangle of given measurement is as follows:
- Draw a line segment AB which is equal to XY + YZ + ZX = 11 cm.
- Make an angle ∠Y = 30° from point A and the angle be ∠LAB
- Make an angle ∠Z = 90° from point B and the angle be ∠MAB
- Bisect ∠LAB and ∠MAB at point X.
- Now take the perpendicular bisector of the line XA and XB and the intersection point be Y and Z respectively.
- Join XY and XZ
- Therefore, XYZ is the required triangle
Q.4: Construct a triangle ABC in which BC = 8cm, ∠B = 45° and AB – AC = 3.5 cm.
Solution:
Construction Procedure:
The steps to draw the triangle of given measurement is as follows:
- Draw a line segment of base BC = 8 cm
- Measure and draw ∠B = 45° and draw the ray BX
- Take a compass and measure AB – AC = 3.5 cm.
- With B as centre and draw an arc at the point be D on the ray BX
- Join DC
- Now draw the perpendicular bisector of the line CD and the intersection point is taken as A.
- Now join AC
- Therefore, ABC is the required triangle.

Q.5: Draw a line segment AB of 4 cm in length. Draw a line perpendicular to AB through A and B, respectively. Are these lines parallel?
Solution:
According to the question,
A line segment AB of length 4cm.
To draw a perpendicular to AB through A and B, respectively.

Steps of construction:
1. Draw AB = 4 cm.
2. With A as centre, draw an arc, intersecting AB at P.
3. With P as centre and the same radius, draw an arc intersecting the arc drawn in step 2 at Q.
4. With Q as centre and the same radius, draw an arc, intersecting the arc drawn in step 3 at R.
5. With R as centre and the same radius, draw an arc, intersecting the arc drawn in step 5 at X.
6. Draw OX and produced it to C and D.
7. Now, repeat the steps from 2 to 7 to draw the line EF perpendicular through B.
Yes, these lines are parallel because the sum of the interior angles on the same side of the transversal is 180 degrees.
Extra Questions To Practice For Class 9 Maths Chapter 11 (CBSE)
- Construct a triangle PQR in which QR = 6cm, ∠Q = 60° and PR – PQ = 2cm.
- Construct a right triangle whose base is 12cm and sum of its hypotenuse and other side is 18 cm.
- Draw an angle of 80° with the help of a protractor. Then construct angles of
- (i) 40°
- (ii)160°
- (iii) 120°
- Construct a triangle whose sides are 3.6 cm, 3.0 cm and 4.8 cm. Bisect the smallest angle and measure each part.
- A triangle if its perimeter is 10.4 cm and two angles are 45° and 120°.