Exercise 13.9 Page No: 236

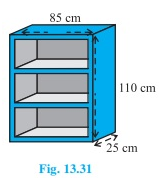
1. A wooden bookshelf has external dimensions as follows: Height = 110cm, Depth = 25cm,

Breadth = 85cm (see fig. 13.31). The thickness of the plank is 5cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is 20 paise per cm² and the rate of painting is 10 paise per cm², find the total expenses required for polishing and painting the surface of the bookshelf.

Solution:

External dimensions of book self,

Length, l = 85cm

Breadth, b = 25 cm

Height, h = 110 cm

External surface area of shelf while leaving out the front face of the shelf

= lh+2(lb+bh)

= [85×110+2(85×25+25×110)] = (9350+9750) = 19100

External surface area of shelf is 19100 cm²

Area of front face = [85×110-75×100+2(75×5)] = 1850+750

So, area is 2600 cm²

Area to be polished = (19100+2600) cm² = 21700 cm².

Cost of polishing 1 cm² area = Rs 0.20

Cost of polishing 21700 cm² area Rs. (21700×0.20) = Rs 4340

Dimensions of row of the book shelf

Length(l) = 75 cm

Breadth (b) = 20 cm and

Height(h) = 30 cm

Area to be painted in one row= 2(l+h)b+lh = [2(75+30)× 20+75×30] = (4200+2250) = 6450

So, area is 6450 cm².

Area to be painted in 3 rows = (3×6450)cm² = 19350 cm².

Cost of painting 1 cm² area = Rs. 0.10

Cost of painting 19350 cm² area = Rs (19350 x 0.1) = Rs 1935

Total expense required for polishing and painting = Rs. (4340+1935) = Rs. 6275

Answer: The cost for polishing and painting the surface of the book shelf is Rs. 6275.

2. The front compound wall of a house is decorated by wooden spheres of diameter 21 cm, placed on small supports as shown in fig. 13.32. Eight such spheres are used forth is purpose, and are to be painted silver. Each support is a cylinder of radius 1.5cm and height 7cm and is to be painted black. Find the cost of paint required if silver paint costs 25 paise per cm² and black paint costs 5 paise per cm².

Solution:

Diameter of wooden sphere = 21 cm

Radius of wooden sphere, r = diameter/ 2 = (21/2) cm = 10.5 cm

Formula: Surface area of wooden sphere = 4πr²

= 4×(22/7)×(10.5)² = 1386

So, surface area is 1386 cm³

Radius of the circular end of cylindrical support = 1.5 cm

Height of cylindrical support = 7 cm

Curved surface area = 2πrh

= 2×(22/7)×1.5×7 = 66

So, CSA is 66 cm²

Now,

Area of the circular end of cylindrical support = πr²

= (22/7)×1.5²

= 7.07

Area of the circular end is 7.07 cm²

Again,

Area to be painted silver = [8 ×(1386-7.07)] = 8×1378.93 = 11031.44

Area to be painted is 11031.44 cm²

Cost for painting with silver colour = Rs(11031.44×0.25) =Rs 2757.86

Area to be painted black = (8×66) cm² = 528 cm²

Cost for painting with black colour =Rs (528×0.05) = Rs26.40

Therefore, the total painting cost is:

= Rs(2757.86 +26.40)

= Rs 2784.26

3. The diameter of a sphere is decreased by 25%. By what percent does its curved surface area decrease?

Solution:

Let the diameter of the sphere be “d”.

Radius of sphere, r₁ = d/2

New radius of sphere, say r₂ = (d/2)×(1-25/100) = 3d/8

Curved surface area of sphere, (CSA)₁ = 4πr₁² = 4π×(d/2)² = πd² …(1)

Curved surface area of sphere when radius is decreased (CSA)₂ = 4πr₂² = 4π×(3d/8)² = (9/16)πd² …(2)

From equation (1) and (2), we have

Decrease in surface area of sphere = (CSA)₁ – (CSA)₂

= πd² – (9/16)πd²

= (7/16)πd²

= (7d²/16d²)×100 = 700/16 = 43.75% .

Therefore, the percentage decrease in the surface area of the sphere is 43.75% .

Important Surface Areas and Volumes Questions For Class 9 (Chapter 13)

Q.1: Hameed has built a cubical water tank with lid for his house, with each outer edge 1.5 m long. He gets the outer surface of the tank excluding the base, covered with square tiles of side 25 cm (see in the figure below). Find how much he would spend on the tiles if the cost of the tiles is Rs.360 per dozen.

Q.2: The paint in a certain container is sufficient to paint an area equal to 9.375 sq.m. How many bricks of dimensions 22.5 cm × 10 cm × 7.5 cm can be painted out of this container?

Q.3: The length, breadth and height of a room are 5 m, 4 m and 3 m respectively. Find the cost of whitewashing the walls of the room and the ceiling at the rate of  Rs.7.50 per sq.m.

Q.4: The curved surface area of a right circular cylinder of height 14 cm is 88 cm. sq. Find the diameter of the base of the cylinder.

Q.5: Curved surface area of a right circular cylinder is 4.4 sq.m. If the radius of the base of the cylinder is 0.7 m, find its height.

Q.6: In a hot water heating system, there is a cylindrical pipe of length 28 m and diameter 5 cm. Find the total radiating surface in the system.

Q.7: The height of a cone is 16 cm and its base radius is 12 cm. Find the curved surface area and the total surface area of the cone.

Q.8: Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m.

Q.9: The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white-washing its curved surface at the rate of Rs.210 per 100 sq.m.

Q.10: The hollow sphere, in which the circus motorcyclist performs his stunts, has a diameter of 7 m. Find the area available to the motorcyclist for riding.