Exercise: 12.1 (Page No: 202)

1. A traffic signal board, indicating ‘SCHOOL AHEAD’, is an equilateral triangle with side ‘a’. Find the area of the signal board, using Heron’s formula. If its perimeter is 180 cm, what will be the area of the signal board?

Solution:

Given,

Side of the signal board = a

Perimeter of the signal board = 3a = 180 cm

∴ a = 60 cm

Semi perimeter of the signal board (s) = 3a/2

By using Heron’s formula,

Area of the triangular signal board will be =

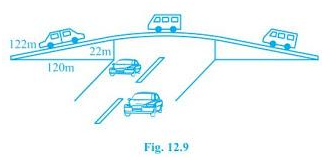
2. The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122 m, 22 m and 120 m (see Fig. 12.9). The advertisements yield an earning of Rs 5000 per m² per year. A company hired one of its walls for 3 months. How much rent did it pay?

Solution:

The sides of the triangle ABC are 122 m, 22 m and 120 m respectively.

Now, the perimeter will be (122+22+120) = 264 m

Also, the semi perimeter (s) = 264/2 = 132 m

Using Heron’s formula,

Area of the triangle =

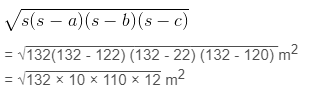
=1320 m²

We know that the rent of advertising per year = Rs 5000 per m²

∴ The rent of one wall for 3 months = Rs. (1320×5000×3)/12 = Rs. 1650000

3. There is a slide in a park. One of its side walls has been painted in some colour with a message “KEEP THE PARK GREEN AND CLEAN” (see Fig. 12.10 ). If the sides of the wall are 15 m, 11 m and 6 m, find the area painted in colour.

Solution:

It is given that the sides of the wall as 15 m, 11 m and 6 m.

So, the semi perimeter of triangular wall (s) = (15+11+6)/2 m = 16 m

Using Heron’s formula,

Area of the message =

= √[16(16-15)(16-11) (16-6)] m²

= √[16×1×5×10] m² = √800 m²

= 20√2 m²

4. Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42cm.

Solution:

Assume the third side of the triangle to be “x”.

Now, the three sides of the triangle are 18 cm, 10 cm, and “x” cm

It is given that the perimeter of the triangle = 42cm

So, x = 42-(18+10) cm = 14 cm

∴ The semi perimeter of triangle = 42/2 = 21 cm

Using Heron’s formula,

Area of the triangle, =

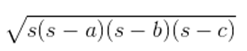
= √[21(21-18)(21-10)(21-14)] cm²

= √[21×3×11×7] m²

= 21√11 cm²

5. Sides of a triangle are in the ratio of 12 : 17 : 25 and its perimeter is 540cm. Find its area.

Solution:

The ratio of the sides of the triangle are given as 12 : 17 : 25

Now, let the common ratio between the sides of the triangle be “x”

∴ The sides are 12x, 17x and 25x

It is also given that the perimeter of the triangle = 540 cm

12x+17x+25x = 540 cm

54x = 540cm

So, x = 10

Now, the sides of triangle are 120 cm, 170 cm, 250 cm.

So, the semi perimeter of the triangle (s) = 540/2 = 270 cm

Using Heron’s formula,

Area of the triangle

= 9000 cm²

6. An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle.

Solution:

First, let the third side be x.

It is given that the length of the equal sides is 12 cm and its perimeter is 30 cm.

So, 30 = 12+12+x

∴ The length of the third side = 6 cm

Thus, the semi perimeter of the isosceles triangle (s) = 30/2 cm = 15 cm

Using Heron’s formula,

Area of the triangle =

= √[15(15-12)(15-12)(15-6)] cm²

= √[15×3×3×9] cm²

= 9√15 cm²