Exercise 9.4(Optional)* Page: 164
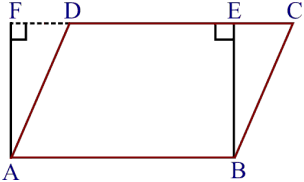
1. Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
Solution:
Given,
|| gm ABCD and a rectangle ABEF have the same base AB and equal areas.
To prove,
Perimeter of || gm ABCD is greater than the perimeter of rectangle ABEF.
Proof,
We know that, the opposite sides of a|| gm and rectangle are equal.
, AB = DC [As ABCD is a || gm]
and, AB = EF [As ABEF is a rectangle]
, DC = EF … (i)
Adding AB on both sides, we get,
⇒AB + DC = AB + EF … (ii)
We know that, the perpendicular segment is the shortest of all the segments that can be drawn to a given line from a point not lying on it.
, BE < BC and AF < AD
⇒ BC > BE and AD > AF
⇒ BC+AD > BE+AF … (iii)
Adding (ii) and (iii), we get
AB+DC+BC+AD > AB+EF+BE+AF
⇒ AB+BC+CD+DA > AB+ BE+EF+FA
⇒ perimeter of || gm ABCD > perimeter of rectangle ABEF.
, the perimeter of the parallelogram is greater than that of the rectangle.
Hence Proved.
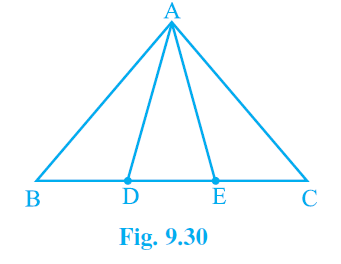
2. In Fig. 9.30, D and E are two points on BC such that BD = DE = EC.
Show that ar (ABD) = ar (ADE) = ar (AEC).
Can you now answer the question that you have left in the ‘Introduction’ of this chapter, whether the field of Budhia has been actually divided into three parts of equal area?
[Remark: Note that by taking BD = DE = EC, the triangle ABC is divided into three triangles ABD, ADE and AEC of equal areas. In the same way, by dividing BC into n equal parts and joining the points of division so obtained to the opposite vertex of BC, you can divide DABC into n triangles of equal areas.]
Solution:
Given,
BD = DE = EC
To prove,
ar (△ABD) = ar (△ADE) = ar (△AEC)
Proof,
In (△ABE), AD is median [since, BD = DE, given]
We know that, the median of a triangle divides it into two parts of equal areas
, ar(△ABD) = ar(△AED) —(i)
Similarly,
In (△ADC), AE is median [since, DE = EC, given]
,ar(ADE) = ar(AEC) —(ii)
From the equation (i) and (ii), we get
ar(ABD) = ar(ADE) = ar(AEC)
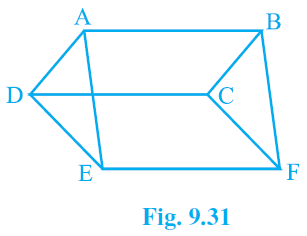
3. In Fig. 9.31, ABCD, DCFE and ABFE are parallelograms. Show that ar (ADE) = ar (BCF).
Solution:
Given,
ABCD, DCFE and ABFE are parallelograms
To prove,
ar (△ADE) = ar (△BCF)
Proof,
In △ADE and △BCF,
AD = BC [Since, they are the opposite sides of the parallelogram ABCD]
DE = CF [Since, they are the opposite sides of the parallelogram DCFE]
AE = BF [Since, they are the opposite sides of the parallelogram ABFE]
, △ADE ≅ △BCF [Using SSS Congruence theorem]
, ar(△ADE) = ar(△BCF) [ By CPCT]
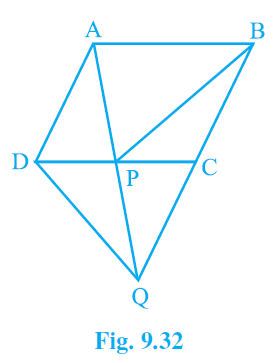
4. In Fig. 9.32, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar (BPC) = ar (DPQ).
[Hint : Join AC.]
Solution:
Given:
ABCD is a parallelogram
AD = CQ
To prove:
ar (△BPC) = ar (△DPQ)
Proof:
In △ADP and △QCP,
∠APD = ∠QPC [Vertically Opposite Angles]
∠ADP = ∠QCP [Alternate Angles]
AD = CQ [given]
, △ABO ≅ △ACD [AAS congruency]
, DP = CP [CPCT]
In △CDQ, QP is median. [Since, DP = CP]
Since, median of a triangle divides it into two parts of equal areas.
, ar(△DPQ) = ar(△QPC) —(i)
In △PBQ, PC is median. [Since, AD = CQ and AD = BC ⇒ BC = QC]
Since, median of a triangle divides it into two parts of equal areas.
, ar(△QPC) = ar(△BPC) —(ii)
From the equation (i) and (ii), we get
ar(△BPC) = ar(△DPQ)
5. In Fig.9.33, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that:
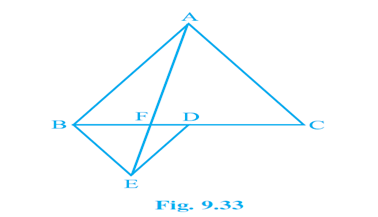
(i) ar (BDE) =1/4 ar (ABC)
(ii) ar (BDE) = ½ ar (BAE)
(iii) ar (ABC) = 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = 1/8 ar (AFC)
Solution:
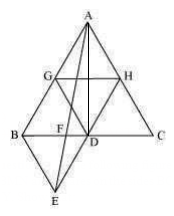
(i) Assume that G and H are the mid-points of the sides AB and AC respectively.
Join the mid-points with line-segment GH. Here, GH is parallel to third side.
, BC will be half of the length of BC by mid-point theorem.

∴ GH =1/2 BC and GH || BD
∴ GH = BD = DC and GH || BD (Since, D is the mid-point of BC)
Similarly,
GD = HC = HA
HD = AG = BG
, ΔABC is divided into 4 equal equilateral triangles ΔBGD, ΔAGH, ΔDHC and ΔGHD
We can say that,
ΔBGD = ¼ ΔABC
Considering, ΔBDG and ΔBDE
BD = BD (Common base)
Since both triangles are equilateral triangle, we can say that,
BG = BE
DG = DE
, ΔBDG ΔBDE [By SSS congruency]
, area (ΔBDG) = area (ΔBDE)
ar (ΔBDE) = ¼ ar (ΔABC)
Hence proved
(ii)
ar(ΔBDE) = ar(ΔAED) (Common base DE and DE||AB)
ar(ΔBDE)−ar(ΔFED) = ar(ΔAED)−ar (ΔFED)
ar(ΔBEF) = ar(ΔAFD) …(i)
Now,
ar(ΔABD) = ar(ΔABF)+ar(ΔAFD)
ar(ΔABD) = ar(ΔABF)+ar(ΔBEF) [From equation (i)]
ar(ΔABD) = ar(ΔABE) …(ii)
AD is the median of ΔABC.
ar(ΔABD) = ½ ar (ΔABC)
= (4/2) ar (ΔBDE)
= 2 ar (ΔBDE)…(iii)
From (ii) and (iii), we obtain
2 ar (ΔBDE) = ar (ΔABE)
ar (BDE) = ½ ar (BAE)
Hence proved
(iii) ar(ΔABE) = ar(ΔBEC) [Common base BE and BE || AC]
ar(ΔABF) + ar(ΔBEF) = ar(ΔBEC)
From eqn (i), we get,
ar(ΔABF) + ar(ΔAFD) = ar(ΔBEC)
ar(ΔABD) = ar(ΔBEC)
½ ar(ΔABC) = ar(ΔBEC)
ar(ΔABC) = 2 ar(ΔBEC)
Hence proved
(iv) ΔBDE and ΔAED lie on the same base (DE) and are in-between the parallel lines DE and AB.
∴ar (ΔBDE) = ar (ΔAED)
Subtracting ar(ΔFED) from L.H.S and R.H.S,
We get,
∴ar (ΔBDE)−ar (ΔFED) = ar (ΔAED)−ar (ΔFED)
∴ar (ΔBFE) = ar(ΔAFD)
Hence proved
(v) Assume that h is the height of vertex E, corresponding to the side BD in ΔBDE.
Also assume that H is the height of vertex A, corresponding to the side BC in ΔABC.
While solving Question (i),
We saw that,
ar (ΔBDE) = ¼ ar (ΔABC)
While solving Question (iv),
We saw that,
ar (ΔBFE) = ar (ΔAFD).
∴ar (ΔBFE) = ar (ΔAFD)
= 2 ar (ΔFED)
Hence, ar (ΔBFE) = 2 ar (ΔFED)
Hence proved
(vi) ar (ΔAFC) = ar (ΔAFD) + ar(ΔADC)
= 2 ar (ΔFED) + (1/2) ar(ΔABC) [using (v)
= 2 ar (ΔFED) + ½ [4ar(ΔBDE)] [Using result of Question (i)]
= 2 ar (ΔFED) +2 ar(ΔBDE)
Since, ΔBDE and ΔAED are on the same base and between same parallels
= 2 ar (ΔFED) +2 ar (ΔAED)
= 2 ar (ΔFED) +2 [ar (ΔAFD) +ar (ΔFED)]
= 2 ar (ΔFED) +2 ar (ΔAFD) +2 ar (ΔFED) [From question (viii)]
= 4 ar (ΔFED) +4 ar (ΔFED)
⇒ar (ΔAFC) = 8 ar (ΔFED)
⇒ar (ΔFED) = (1/8) ar (ΔAFC)
Hence proved
6. Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that
ar (APB)×ar (CPD) = ar (APD)×ar (BPC).
[Hint : From A and C, draw perpendiculars to BD.]
Solution:
Given:
The diagonal AC and BD of the quadrilateral ABCD, intersect each other at point E.
Construction:
From A, draw AM perpendicular to BD
From C, draw CN perpendicular to BD
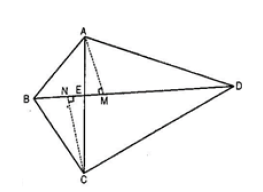
To Prove,
ar(ΔAED) ar(ΔBEC) = ar (ΔABE) ×ar (ΔCDE)
Proof,
ar(ΔABE) = ½ ×BE×AM………….. (i)
ar(ΔAED) = ½ ×DE×AM………….. (ii)
Dividing eq. ii by i , we get,
ar(AED)/ar(ABE) = DE/BE…….. (iii)
Similarly,
ar(CDE)/ar(BEC) = DE/BE ……. (iv)
From eq. (iii) and (iv) , we get
ar(AED)/ar(ABE) = ar(CDE)/ar(BEC)
, ar(ΔAED)×ar(ΔBEC) = ar(ΔABE)×ar (ΔCDE)
Hence proved.
7. P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that:
(i) ar (PRQ) = ½ ar (ARC)
(ii) ar (RQC) = (3/8) ar (ABC)
(iii) ar (PBQ) = ar (ARC)
Solution:
(i)

We know that, median divides the triangle into two triangles of equal area,
PC is the median of ABC.
Ar (ΔBPC) = ar (ΔAPC) ……….(i)
RC is the median of APC.
Ar (ΔARC) = ½ ar (ΔAPC) ……….(ii)
PQ is the median of BPC.
Ar (ΔPQC) = ½ ar (ΔBPC) ……….(iii)
From eq. (i) and (iii), we get,
ar (ΔPQC) = ½ ar (ΔAPC) ……….(iv)
From eq. (ii) and (iv), we get,
ar (ΔPQC) = ar (ΔARC) ……….(v)
P and Q are the mid-points of AB and BC respectively [given]
PQ||AC
and, PA = ½ AC
Since, triangles between same parallel are equal in area, we get,
ar (ΔAPQ) = ar (ΔPQC) ……….(vi)
From eq. (v) and (vi), we obtain,
ar (ΔAPQ) = ar (ΔARC) ……….(vii)
R is the mid-point of AP.
, RQ is the median of APQ.
Ar (ΔPRQ) = ½ ar (ΔAPQ) ……….(viii)
From (vii) and (viii), we get,
ar (ΔPRQ) = ½ ar (ΔARC)
Hence Proved.
(ii) PQ is the median of ΔBPC
ar (ΔPQC) = ½ ar (ΔBPC)
= (½) ×(1/2 )ar (ΔABC)
= ¼ ar (ΔABC) ……….(ix)
Also,
ar (ΔPRC) = ½ ar (ΔAPC) [From (iv)]
ar (ΔPRC) = (1/2)×(1/2)ar ( ABC)
= ¼ ar(ΔABC) ……….(x)
Add eq. (ix) and (x), we get,
ar (ΔPQC) + ar (ΔPRC) = (1/4)×(1/4)ar (ΔABC)
ar (quad. PQCR) = ¼ ar (ΔABC) ……….(xi)
Subtracting ar (ΔPRQ) from L.H.S and R.H.S,
ar (quad. PQCR)–ar (ΔPRQ) = ½ ar (ΔABC)–ar (ΔPRQ)
ar (ΔRQC) = ½ ar (ΔABC) – ½ ar (ΔARC) [From result (i)]
ar (ΔARC) = ½ ar (ΔABC) –(1/2)×(1/2)ar (ΔAPC)
ar (ΔRQC) = ½ ar (ΔABC) –(1/4)ar (ΔAPC)
ar (ΔRQC) = ½ ar (ΔABC) –(1/4)×(1/2)ar (ΔABC) [ As, PC is median of ΔABC]
ar (ΔRQC) = ½ ar (ΔABC)–(1/8)ar (ΔABC)
ar (ΔRQC) = [(1/2)-(1/8)]ar (ΔABC)
ar (ΔRQC) = (3/8)ar (ΔABC)
(iii) ar (ΔPRQ) = ½ ar (ΔARC) [From result (i)]
2ar (ΔPRQ) = ar (ΔARC) ……………..(xii)
ar (ΔPRQ) = ½ ar (ΔAPQ) [RQ is the median of APQ] ……….(xiii)
But, we know that,
ar (ΔAPQ) = ar (ΔPQC) [From the reason mentioned in eq. (vi)] ……….(xiv)
From eq. (xiii) and (xiv), we get,
ar (ΔPRQ) = ½ ar (ΔPQC) ……….(xv)
At the same time,
ar (ΔBPQ) = ar (ΔPQC) [PQ is the median of ΔBPC] ……….(xvi)
From eq. (xv) and (xvi), we get,
ar (ΔPRQ) = ½ ar (ΔBPQ) ……….(xvii)
From eq. (xii) and (xvii), we get,
2×(1/2)ar(ΔBPQ)= ar (ΔARC)
⟹ ar (ΔBPQ) = ar (ΔARC)
Hence Proved.
8. In Fig. 9.34, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ^ DE meets BC at Y. Show that:
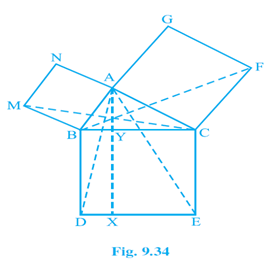
(i) ΔMBC ≅ ΔABD
(ii) ar(BYXD) = 2ar(MBC)
(iii) ar(BYXD) = ar(ABMN)
(iv) ΔFCB ≅ ΔACE
(v) ar(CYXE) = 2ar(FCB)
(vi) ar(CYXE) = ar(ACFG)
(vii) ar(BCED) = ar(ABMN)+ar(ACFG)
Note : Result (vii) is the famous Theorem of Pythagoras. You shall learn a simpler proof of this theorem in Class X.
Solution:
(i) We know that each angle of a square is 90°. Hence, ∠ABM = ∠DBC = 90º
∴∠ABM+∠ABC = ∠DBC+∠ABC
∴∠MBC = ∠ABD
In ∆MBC and ∆ABD,
∠MBC = ∠ABD (Proved above)
MB = AB (Sides of square ABMN)
BC = BD (Sides of square BCED)
∴ ∆MBC ≅ ∆ABD (SAS congruency)
(ii) We have
∆MBC ≅ ∆ABD
∴ar (∆MBC) = ar (∆ABD) … (i)
It is given that AX ⊥ DE and BD ⊥ DE (Adjacent sides of square BDEC)
∴ BD || AX (Two lines perpendicular to same line are parallel to each other)
∆ABD and parallelogram BYXD are on the same base BD and between the same parallels BD and AX.
Area (∆YXD) = 2 Area (∆MBC) [From equation (i)] … (ii)
(iii) ∆MBC and parallelogram ABMN are lying on the same base MB and between same parallels MB and NC.
2 ar (∆MBC) = ar (ABMN)
ar (∆YXD) = ar (ABMN) [From equation (ii)] … (iii)
(iv) We know that each angle of a square is 90°.
∴∠FCA = ∠BCE = 90º
∴∠FCA+∠ACB = ∠BCE+∠ACB
∴∠FCB = ∠ACE
In ∆FCB and ∆ACE,
∠FCB = ∠ACE
FC = AC (Sides of square ACFG)
CB = CE (Sides of square BCED)
∆FCB ≅ ∆ACE (SAS congruency)
(v) AX ⊥ DE and CE ⊥ DE (Adjacent sides of square BDEC) [given]
Hence,
CE || AX (Two lines perpendicular to the same line are parallel to each other)
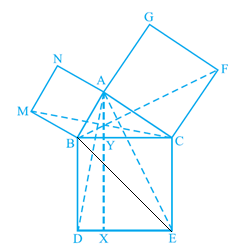
Consider BACE and parallelogram CYXE
BACE and parallelogram CYXE are on the same base CE and between the same parallels CE and AX.
∴ar (∆YXE) = 2ar (∆ACE) … (iv)
We had proved that
∴ ∆FCB ≅ ∆ACE
ar (∆FCB) ≅ ar (∆ACE) … (v)
From equations (iv) and (v), we get
ar (CYXE) = 2 ar (∆FCB) … (vi)
(vi) Consider BFCB and parallelogram ACFG
BFCB and parallelogram ACFG are lying on the same base CF and between the same parallels CF and BG.
∴ar (ACFG) = 2 ar (∆FCB)
∴ar (ACFG) = ar (CYXE) [From equation (vi)] … (vii)
(vii) From the figure, we can observe that
ar (∆CED) = ar (∆YXD)+ar (CYXE)
∴ar (∆CED) = ar (ABMN)+ar (ACFG) [From equations (iii) and (vii)].
Extra Questions for Class 9 Maths Chapter 9
- P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB) = ar(BQC).
- PQRS and ABRS are parallelograms and X is any point on side BR. Show that:
- ar(PQRS) = ar(ABRS)
- ar (AXS) = ½ ar(PQRS)
- A farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to points P and Q. In how many parts the fields is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it?
- In Figure, E is any point on median AD of a ΔABC. Show that ar (ABE) =
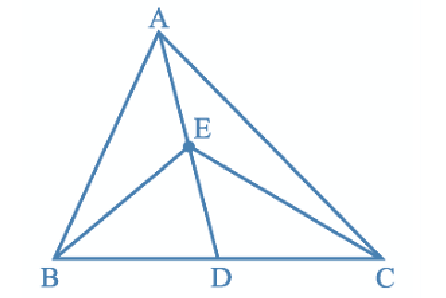
- ar(ACE).
- Show that the diagonals of a parallelogram divide it into four triangles of equal area.
- D and E are points on sides AB and AC respectively of ΔABC such that ar(DBC) = ar(EBC). Prove that DE || BC.
- The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed (see in the figure). Show that:
- ar(ABCD) = ar(PBQR).
- [Hint: Join AC and PQ. Now compare ar(ACQ) and ar(APQ).]
- Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar (AOD) = ar (BOC).