Exercise: 10.6 (Page No: 186)

1.  Prove that the line of centres of two intersecting circles subtends equal angles at the two points of intersection.

Solution:

Consider the following diagram

In ΔPOO’ and ΔQOO’

OP = OQ          (Radius of circle 1)

O’P = O’Q        (Radius of circle 2)

OO’ = OO’        (Common arm)

So, by SSS congruency, ΔPOO’ ≅ ΔQOO’

Thus, ∠OPO’ = ∠OQO’ (proved).

2. Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are on opposite sides of its centre. If the distance between AB and CD is 6 , find the radius of the circle.

Solution:

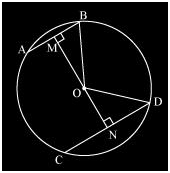
Here, OM ⊥ AB and ON ⊥ CD. is drawn and OB and OD are joined.

We know that AB bisects BM as the perpendicular from the centre bisects chord.

Since AB = 5 so,

BM = AB/2

Similarly, ND = CD/2 = 11/2

Now, let ON be x.

So, OM = 6−x.

Consider ΔMOB,

OB² = OM²+MB²

Or,

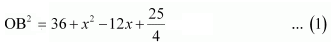
Consider ΔNOD,

OD² = ON² + ND²

Or

We know, OB = OD (radii)

From equation 1 and equation 2 we get

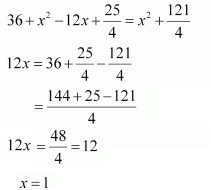
Now, from equation (2) we have,

OD²= 1² +(121/4)

Or OD = (5/2)×√5 cm

3. The lengths of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at a distance 4 cm from the centre, what is the distance of the other chord from the centre?

Solution:

Consider the following diagram

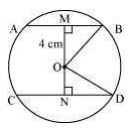
Here AB and CD are 2 parallel chords. Now, join OB and OD.

Distance of smaller chord AB from the centre of the circle = 4 cm

So, OM = 4 cm

MB = AB/2 = 3 cm

Consider ΔOMB

OB² = OM²+MB²

Or, OB = 5cm

Now, consider ΔOND,

OB = OD = 5 (since they are the radii)

ND = CD/2 = 4 cm

Now, OD²= ON²+ND²

Or, ON = 3 cm.

4. Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.

Solution:

Consider the diagram

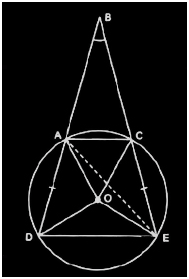
Here AD = CE

We know, any exterior angle of a triangle is equal to the sum of interior opposite angles.

So,

∠DAE = ∠ABC+∠AEC (in ΔBAE) ——————-(i)

DE subtends ∠DOE at the centre and ∠DAE in the remaining part of the circle.

So,

∠DAE = (½)∠DOE ——————-(ii)

Similarly, ∠AEC = (½)∠AOC  ——————-(ii)

Now, from equation (i), (ii), and (iii) we get,

∠DOE = ∠ABC+(½)∠AOC

Or, ∠ABC = (½)[∠DOE-∠AOC]  (hence proved).

5. Prove that the circle drawn with any side of a rhombus as diameter, passes through the point of intersection of its diagonals.

Solution:

To prove: A circle drawn with Q as centre, will pass through A, B and O (i.e. QA = QB = QO)

Since all sides of a rhombus are equal,

AB = DC

Now, multiply (½) on both sides

(½)AB = (½)DC

So, AQ = DP

BQ = DP

Since Q is the midpoint of AB,

AQ= BQ

Similarly,

RA = SB

Again, as PQ is drawn parallel to AD,

RA = QO

Now, as AQ = BQ and RA = QO we get,

QA = QB = QO (hence proved).

6. ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE, = AD.

Solution:

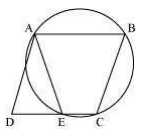
Here, ABCE is a cyclic quadrilateral. In a cyclic quadrilateral, the sum of the opposite angles is 180°.

So, ∠AEC+∠CBA = 180°

As ∠AEC and ∠AED are linear pair,

∠AEC+∠AED = 180°

Or, ∠AED = ∠CBA … (1)

We know in a parallelogram; opposite angles are equal.

So, ∠ADE = ∠CBA … (2)

Now, from equations (1) and (2) we get,

∠AED = ∠ADE

Now, AD and AE are angles opposite to equal sides of a triangle,

∴ AD = AE (proved).

7. AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters; (ii) ABCD is a rectangle.

Solution:

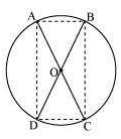
Here chords AB and CD intersect each other at O.

Consider ΔAOB and ΔCOD,

∠AOB = ∠COD (They are vertically opposite angles)

OB = OD (Given in the question)

OA = OC (Given in the question)

So, by SAS congruency, ΔAOB ≅ ΔCOD

Also, AB = CD (By CPCT)

Similarly, ΔAOD ≅ ΔCOB

Or, AD = CB (By CPCT)

In quadrilateral ACBD, opposite sides are equal.

So, ACBD is a parallelogram.

We know that opposite angles of a parallelogram are equal.

So, ∠A = ∠C

Also, as ABCD is a cyclic quadrilateral,

∠A+∠C = 180°

⇒∠A+∠A = 180°

Or, ∠A = 90°

As ACBD is a parallelogram and one of its interior angles is 90°, so, it is a rectangle.

∠A is the angle subtended by chord BD. And as ∠A = 90°, therefore, BD should be the diameter of the circle. Similarly, AC is the diameter of the circle.

8. Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are 90°–(½)A, 90°–(½)B and 90°–(½)C.

Solution:

Consider the following diagram

Here, ABC is inscribed in a circle with center O and the bisectors of ∠A, ∠B and ∠C intersect the circumcircle at D, E and F respectively.

Now, join DE, EF and FD

As angles in the same segment are equal, so,

∠FDA = ∠FCA ————-(i)

∠FDA = ∠EBA ————-(i)

By adding equations (i) and (ii) we get,

∠FDA+∠EDA = ∠FCA+∠EBA

Or, ∠FDE = ∠FCA+∠EBA = (½)∠C+(½)∠B

We know, ∠A +∠B+∠C = 180°

So, ∠FDE = (½)[∠C+∠B] = (½)[180°-∠A]

∠FDE = [90-(∠A/2)]

In a similar way,

∠FED = [90° -(∠B/2)] °

And,

∠EFD = [90° -(∠C/2)] °

9. Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.

Solution:

The diagram will be

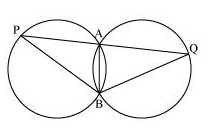
Here, ∠APB = ∠AQB (as AB is the common chord in both the congruent circles.)

Now, consider ΔBPQ,

∠APB = ∠AQB

So, the angles opposite to equal sides of a triangle.

∴ BQ = BP

10. In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.

Solution:

Consider this diagram

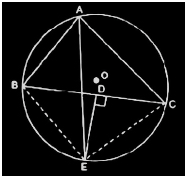
Here, join BE and CE.

Now, since AE is the bisector of ∠BAC,

∠BAE = ∠CAE

Also,

∴arc BE = arc EC

This implies, chord BE = chord EC

Now, consider triangles ΔBDE and ΔCDE,

DE = DE     (It is the common side)

BD = CD     (It is given in the question)

BE = CE      (Already proved)

So, by SSS congruency, ΔBDE ΔCDE.

Thus, ∴∠BDE = ∠CDE

We know, ∠BDE = ∠CDE = 180°

Or, ∠BDE = ∠CDE = 90°

∴ DE ⊥ BC (hence proved).

Extra Questions (CBSE) For Class 9 Maths Chapter 10

1. Recall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.
2. Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
3. If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
4. If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD
5. Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6m each, what is the distance between Reshma and Mandip?
6. In Fig. 10.36, A,B and C are three points on a circle with centre O such that ∠BOC = 30° and ∠AOB = 60°. If D is a point on the circle other than the arc ABC, find ∠ADC. 

1. A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
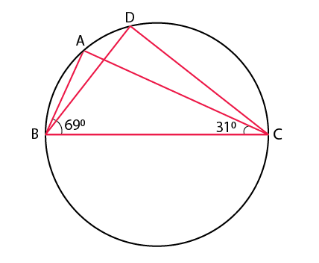
2. In Figure, ∠ABC = 69°, ∠ ACB = 31°, find ∠BDC. 

1. Prove that a cyclic parallelogram is a rectangle.
2. Let the vertex of an angle ABC be located outside a circle and let the sides of the angle intersect equal chords AD and CE with the circle. Prove that ∠ABC is equal to half the difference of the angles subtended by the chords AC and DE at the centre.
3. ABCD is a parallelogram. The circle through A, B and C intersect CD (produced if necessary) at E. Prove that AE, = AD.
4. AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters; (ii) ABCD is a rectangle.