Introduction to Heron’s Formula
Triangle
The plane closed figure, with three sides and three angles is called as a triangle.
Types of triangles:
Based on sides – a) Equilateral b) Isosceles c) Scalene
Based on angles – a) Acute angled triangle b) Right-angled triangle c) Obtuse angled triangle
Area of a triangle
Area=(1/2)×base×height
In case of equilateral and isosceles triangles, if the length of the sides of triangles are given then,
we use Pythagoras theorem in order to find the height of a triangle.
Area of an equilateral triangle
Consider an equilateral ΔABC, with each side as a unit. Let AO be the perpendicular bisector of BC. In order to derive the formula for the area of an equilateral triangle, we need to find height AO.
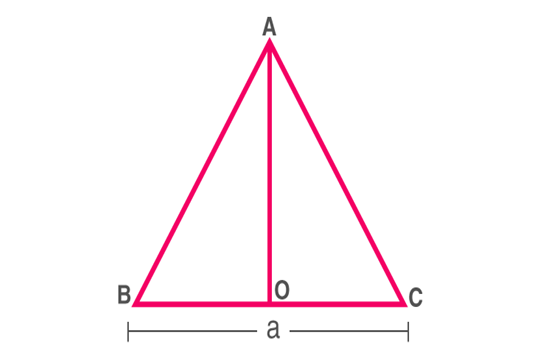
Using Pythagoras theorem,
AC2=OA2+OC2
OA2=AC2−OC2
Substitute AC=a,OC= a/2 to find OA
OA2=a2−a2/4
OA=√3a/2
We know the area of the triangle is
A=(1/2)×base×height,
A=(1/2)×a×(√3a/2)
∴Area of Equilateral triangle=√3a2/4
Area of an isosceles triangle
Consider an isosceles ΔABC with equal sides as a units and base as b units.
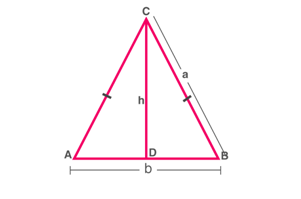
Isosceles triangle ABC
The height of the triangle can be found by Pythagoras’ Theorem :
CD2=AC2−AD2
⇒h2=a2− (b2/4) = (4a2–b2)/4
⇒h=(1/2) √(4a2–b2)
Area of triangle is A=(1/2)bh
∴A=(1/2)×b×(1/2)√(4a2–b2)
∴A=(1/4)×b×√(4a2–b2)
Area of a triangle – By Heron’s formula
Area of a ΔABC, given sides a, b, c by Heron’s formula (Also known as Hero’s Formula) :

Triangle ABC
Find semi perimeter (s ) = (a+b+c)/2
Area=√[s(s-a)(s-b)(s-c)]
This formula is helpful to find the area of a scalene triangle, given the lengths of all its sides.
Area of any polygon – By Heron’s formula
To find the area of a quadrilateral, when one of its diagonal value and the sides are given, the area can be calculated by splitting the given quadrilateral into two triangles and use the Heron’s formula.
Example :A park, in the shape of a quadrilateral ABCD, has ∠C=90∘, AB = 9 cm, BC = 12 cm, CD = 5 cm and AD = 8 cm. How much area does it occupy?
⇒We draw the figure according to the information given.

The figure can be split into 2 triangles ΔBCD and ΔABD
From ΔBCD, we can find BD (Using Pythagoras’ Theorem)
BD2=122+52=169
BD=13cm
Semi-perimeter for ΔBCD S1= (12+5+13)/2 = 15
Semi-perimeter ΔABD S2= (9+8+13)/2 = 15
Using Heron’s formula we find A1 and A2
A1= √[15(15-12)(15-5)(15-13)]
A1= √(15×3×10×2 )
A1=√900 = 30 cm2
Similarly, we find A2 to be 35.49 cm2.
The area of the quadrilateral ABCD=A1+A2=65.49 cm2