Exercise 4.1 Page: 68
1. The cost of a notebook is twice the cost of a pen. Write a linear equation in two variables to represent this statement.
(Take the cost of a notebook to be Rs x and that of a pen to be Rs y)
Solution:
Let the cost of a notebook to be = Rs x
Let the cost of a pen to be = Rs y
According to the question,
The cost of a notebook is twice the cost of a pen.
i.e., Cost of a notebook = 2×Cost of a pen
x = 2×y
x = 2y
x-2y = 0
x-2y = 0 is the linear equation in two variables to represent the statement ‘The cost of a notebook is twice the cost of a pen’.
2. Express the following linear equations in the form ax + by + c = 0 and indicate the values of a, b and c in each case:
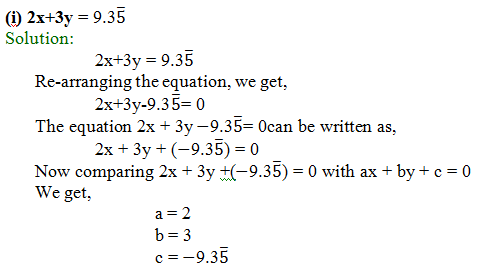
(ii) x –(y/5)–10 = 0
Solution:
The equation x –(y/5)-10 = 0 can be written as,
1x+(-1/5)y +(–10) = 0
Now comparing x+(-1/5)y+(–10) = 0 with ax+by+c = 0
We get,
a = 1
b = -(1/5)
c = -10
(iii) –2x+3y = 6
Solution:
–2x+3y = 6
Re-arranging the equation, we get,
–2x+3y–6 = 0
The equation –2x+3y–6 = 0 can be written as,
(–2)x+3y+(– 6) = 0
Now comparing (–2)x+3y+(–6) = 0 with ax+by+c = 0
We get, a = –2
b = 3
c =6
(iv) x = 3y
Solution:
x = 3y
Re-arranging the equation, we get,
x-3y = 0
The equation x-3y=0 can be written as,
1x+(-3)y+(0)c = 0
Now comparing 1x+(-3)y+(0)c = 0 with ax+by+c = 0
We get, a = 1
b = -3
c =0
(v) 2x = –5y
Solution:
2x = –5y
Re-arranging the equation, we get,
2x+5y = 0
The equation 2x+5y = 0 can be written as,
2x+5y+0 = 0
Now comparing 2x+5y+0= 0 with ax+by+c = 0
We get, a = 2
b = 5
c = 0
(vi) 3x+2 = 0
Solution:
3x+2 = 0
The equation 3x+2 = 0 can be written as,
3x+0y+2 = 0
Now comparing 3x+0+2= 0 with ax+by+c = 0
We get, a = 3
b = 0
c = 2
(vii) y–2 = 0
Solution:
y–2 = 0
The equation y–2 = 0 can be written as,
0x+1y+(–2) = 0
Now comparing 0x+1y+(–2) = 0with ax+by+c = 0
We get, a = 0
b = 1
c = –2
(viii) 5 = 2x
Solution:
5 = 2x
Re-arranging the equation, we get,
2x = 5
i.e., 2x–5 = 0
The equation 2x–5 = 0 can be written as,
2x+0y–5 = 0
Now comparing 2x+0y–5 = 0 with ax+by+c = 0
We get, a = 2
b = 0
c = -5