Exercise 9.2 Page: 159

1. In Fig. 9.15, ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.

Solution:

Given,

AB = CD = 16 cm (Opposite sides of a parallelogram)

CF = 10 cm and AE = 8 cm

Now,

Area of parallelogram = Base × Altitude

= CD×AE = AD×CF

⇒ 16×8 = AD×10

⇒ AD = 128/10 cm

⇒ AD = 12.8 cm

2. If E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar (EFGH) = 1/2 ar(ABCD).

Solution:

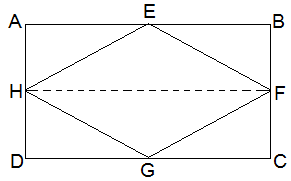
Given,

E, F, G and H are the mid-points of the sides of a parallelogram ABCD respectively.

To Prove,

ar (EFGH) = ½ ar(ABCD)

Construction,

H and F are joined.

Proof,

AD || BC and AD = BC (Opposite sides of a parallelogram)

⇒ ½ AD = ½ BC

Also,

AH || BF and and DH || CF

⇒ AH = BF and DH = CF (H and F are mid points)

∴, ABFH and HFCD are parallelograms.

Now,

We know that, ΔEFH and parallelogram ABFH, both lie on the same FH the common base and in-between the same parallel lines AB and HF.

∴ area of EFH = ½ area of ABFH — (i)

And, area of GHF = ½ area of HFCD — (ii)

Adding (i) and (ii),

area of ΔEFH + area of ΔGHF = ½ area of ABFH + ½ area of HFCD

⇒ area of EFGH = area of ABFH

∴ ar (EFGH) = ½ ar(ABCD)

3. P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD.

Show that ar(APB) = ar(BQC).

Solution:

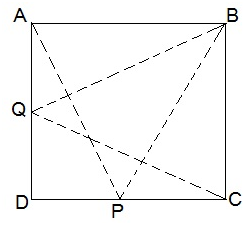
ΔAPB and parallelogram ABCD lie on the same base AB and in-between same parallel AB and DC.

ar(ΔAPB) = ½ ar(parallelogram ABCD) — (i)

Similarly,

ar(ΔBQC) = ½ ar(parallelogram ABCD) — (ii)

From (i) and (ii), we have

ar(ΔAPB) = ar(ΔBQC)

4. In Fig. 9.16, P is a point in the interior of a parallelogram ABCD. Show that

(i) ar(APB) + ar(PCD) = ½ ar(ABCD)

(ii) ar(APD) + ar(PBC) = ar(APB) + ar(PCD)

[Hint : Through P, draw a line parallel to AB.]

Solution:

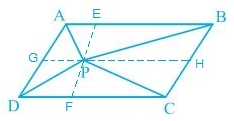
(i) A line GH is drawn parallel to AB passing through P.

In a parallelogram,

AB || GH (by construction) — (i)

∴,

AD || BC ⇒ AG || BH — (ii)

From equations (i) and (ii),

ABHG is a parallelogram.

Now,

ΔAPB and parallelogram ABHG are lying on the same base AB and in-between the same parallel lines AB and GH.

∴ ar(ΔAPB) = ½ ar(ABHG) — (iii)

also,

ΔPCD and parallelogram CDGH are lying on the same base CD and in-between the same parallel lines CD and GH.

∴ ar(ΔPCD) = ½ ar(CDGH) — (iv)

Adding equations (iii) and (iv),

ar(ΔAPB) + ar(ΔPCD) = ½ [ar(ABHG)+ar(CDGH)]

⇒ ar(APB)+ ar(PCD) = ½ ar(ABCD)

(ii) A line EF is drawn parallel to AD passing through P.

In the parallelogram,

AD || EF (by construction) — (i)

∴,

AB || CD ⇒ AE || DF — (ii)

From equations (i) and (ii),

AEDF is a parallelogram.

Now,

ΔAPD and parallelogram AEFD are lying on the same base AD and in-between the same parallel lines AD and EF.

∴ar(ΔAPD) = ½ ar(AEFD) — (iii)

also,

ΔPBC and parallelogram BCFE are lying on the same base BC and in-between the same parallel lines BC and EF.

∴ar(ΔPBC) = ½ ar(BCFE) — (iv)

Adding equations (iii) and (iv),

ar(ΔAPD)+ ar(ΔPBC) = ½ {ar(AEFD)+ar(BCFE)}

⇒ar(APD)+ar(PBC) = ar(APB)+ar(PCD)

5. In Fig. 9.17, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
(i) ar (PQRS) = ar (ABRS)
(ii) ar (AXS) = ½ ar (PQRS) 

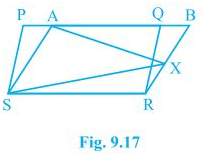
Solution:

(i) Parallelogram PQRS and ABRS lie on the same base SR and in-between the same parallel lines SR and PB.

∴ ar(PQRS) = ar(ABRS) — (i)

(ii) ΔAXS and parallelogram ABRS are lying on the same base AS and in-between the same parallel lines AS and BR.

∴ ar(ΔAXS) = ½ ar(ABRS) — (ii)

From (i) and (ii), we find that,

ar(ΔAXS) = ½ ar(PQRS)

6. A farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to points P and Q. In how many parts the fields is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it?

Solution:

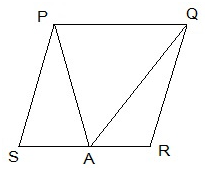
The field is divided into three parts each in triangular shape.

Let, ΔPSA, ΔPAQ and ΔQAR be the triangles.

Area of ΔPSA + ΔPAQ + ΔQAR = Area of PQRS — (i) 

Area of ΔPAQ = ½ area of PQRS — (ii)

Here, the triangle and parallelogram are on the same base and in-between the same parallel lines.

From (i) and (ii),

Area of ΔPSA +Area of ΔQAR = ½ area of PQRS — (iii)

From (ii) and (iii), we can conclude that,

The farmer must sow wheat or pulses in ΔPAQ or either in both ΔPSA and ΔQAR.