Course Content
Class 11 Physics Chapter 1 Physical World
Section Name Topic Name 1 Physical World 1.1 What is physics? 1.2 Scope and excitement of physics 1.3 Physics, technology and society 1.4 Fundamental forces in nature 1.5 Nature of physical laws
0/7
Science and its origin || Natural Sciences || Physics
13:20
Scope of Physics || Macroscopic Domain || Microscopic Domain
Factors responsible for progress of Physics || Technological applications of Physics
Fundamental Forces in nature
Conserved Quantities || Conservation Laws
NCERT Solution of Physical World
Question Bank For NEET | JEE | AIIMS
Class 11 Physics Chapter 2 Unit and Measurements
Unit and Measurements
0/11
Unit
16:57
Measurement of Length || Measuring large Distances – Parallax Method || Measuring very small distances
Special Length units || Measurement of Mass || Measurement of Time
Accuracy and Precision of Instruments || Types of Errors- Systematic Errors || Random Errors
Errors in a series of Measurements
Significant Figures || Rules for Arithmetic operation with Significant Figures || Rules for Rounding off the uncertain digits
Rules for determining uncertainty in results of arithmetic calculations
Dimensions of a Physical Quantity || Dimensional Formula and Dimensional Equation || Applications of Dimensional Analysis
Unit and Measurement NCERT Solution
Unit & Measurement Question Bank For NEET || JEE || AIIMS
Important Extra Questions Physics Chapter 2 Unit and Measurements
Class 11 Physics Chapter 3 Motion In A Straight Line
Section Name Topic Name 3 Motion in a Straight Line 3.1 Introduction 3.2 Position, path length and displacement 3.3 Average velocity and average speed 3.4 Instantaneous velocity and speed 3.5 Acceleration 3.6 Kinematic equations for uniformly accelerated motion 3.7 Relative velocity
0/7
Motion || Frame of Reference || Motion along Straight Line
14:37
Path Length (Distance) Vs. Displacement || Position-Time, Velocity-Time and Acceleration-Time Graph || Average Velocity and Average Speed
Instantaneous Velocity and Instantaneous Speed || Acceleration || Kinematic Equations for Uniformly accelerated Motion
Relative Velocity
NCERT Solutions for Class 11 Physics Chapter 3 Motion In Straight Line
Class 11 Physics Chapter 3 Important Extra Questions Motion in a Straight Line
Motion in Straight Line Question Bank AIIMS || JEE || NEET
Class 11 Physics Chapter 4 Motion In A Plane
4 Motion in a plane 4.1 Introduction 4.2 Scalars and vectors 4.3 Multiplication of vectors by real numbers 4.4 Addition and subtraction of vectors – graphical method 4.5 Resolution of vectors 4.6 Vector addition – analytical method 4.7 Motion in a plane 4.8 Motion in a plane with constant acceleration 4.9 Relative velocity in two dimensions 4.10 Projectile motion 4.11 Uniform circular motion
0/8
Scalars Vs. Vectors || Position and Displacement Vectors || Free and Localized Vectors
11:49
Equality of Vectors || Multiplication of Vectors with real numbers
Addition and Subtraction of Vectors – Triangle Method || Addition of Vectors – Parallelogram Method || Resolution Vector
Unit Vectors || Quantities Related to motion of an object in a plane
Motion in a plane with constant acceleration || Relative velocity in two dimensions
Projectile Motion
Uniform circular motion
NCERT Solutions for Class 11 Physics Chapter 4 Motion in a plane
Class 11 Physics Chapter 5 Laws of motion
Section Name Topic Name 5 Laws of motion 5.1 Introduction 5.2 Aristotle’s fallacy 5.3 The law of inertia 5.4 Newton’s first law of motion 5.5 Newton’s second law of motion 5.6 Newton’s third law of motion 5.7 Conservation of momentum 5.8 Equilibrium of a particle 5.9 Common forces in mechanics 5.10 Circular motion 5.11 Solving problems in mechanics
0/8
INTRODUCTION || Contact & Non-contact forces || Aristotle’s fallacy
21:10
Inertia || Galileo’s Law of Inertia
Newton’s Law of Motion || Momentum || Balance & Unbalanced Force
Conservation of Momentum || Collision of Body || Equilibrium of Particles
Friction
Circular Motion
NCERT SOLUTION OF CLASS 11TH PHYSICS LAW OF MOTION
Law of Motion Question Bank || NEET | JEE || AIIMS
Class 11 Physics Chapter 6 Work Energy and Power
Section Name Topic Name 6 Work Energy and power 6.1 Introduction 6.2 Notions of work and kinetic energy : The work-energy theorem 6.3 Work 6.4 Kinetic energy 6.5 Work done by a variable force 6.6 The work-energy theorem for a variable force 6.7 The concept of potential energy 6.8 The conservation of mechanical energy 6.9 The potential energy of a spring 6.10 Various forms of energy : the law of conservation of energy 6.11 Power 6.12 Collisions
0/8
Introduction || Scalar product
19:02
Notions of Work and Kinetic Energy || Work || Kinetic energy
The Work-Energy Theorem for a Variable Force
Conservative & Non-Conservative Forces|| The Conservation of Mechanical Energy || Potential energy of spring
Chemical Energy || Nuclear Energy
The Equivalence of Mass and Energy || Principle of Conservation of Energy || Power || Collision
NCERT Solutions for Class 11 Physics Chapter 6 Work Energy and Power
Work, Energy & Power Question For NEET || JEE || AIIMS
Class 11 Physics Chapter 7 Rotation motion
Topics Introduction Centre of mass Motion of COM Linear Momentum of System of Particles Vector Product Angular velocity Torque & Angular Momentum Conservation of Angular Momentum Equilibrium of Rigid Body Centre of Gravity Moment of Inertia Theorem of perpendicular axis Theorem of parallel axis Moment of Inertia of Objects Kinematics of Rotational Motion about a Fixed Axis Dynamics of Rotational Motion about a Fixed Axis Angular Momentum In Case of Rotation about a Fixed Axis Rolling motion
0/6
Introduction || Center of Mass || Motion of COM
23:54
Linear Momentum of System of Particles || Vector Product || Angular velocity & its relation with linear velocity
Torque & Angular Momentum || Conservation of Angular Momentum || Equilibrium of Rigid Body
Centre of Gravity || Moment of Inertia || Theorem of perpendicular axis || Theorem of parallel axis || Kinematics of Rotational Motion about a Fixed Axis
Dynamics of Rotational Motion about a Fixed Axis || Rolling Motion
NCERT Solutions for Class 11 Physics Chapter 7 System of Particles and Rotational Motion
Class 11 Physics Chapter 8 Gravitation
Section Name Topic Name 8 Gravitation 8.1 Introduction 8.2 Kepler’s laws 8.3 Universal law of gravitation 8.4 The gravitational constant 8.5 Acceleration due to gravity of the earth 8.6 Acceleration due to gravity below and above the surface of earth 8.7 Gravitational potential energy 8.8 Escape speed 8.9 Earth satellite 8.10 Energy of an orbiting satellite 8.11 Geostationary and polar satellites 8.12 Weightlessness
0/8
Introduction || Gravitational Constant || Newton’s View of Gravitation || Universal Law of Gravitation || Gravitational Constant: Cavendish experiment || Acceleration due to gravity of the earth
17:12
Expression for Acceleration due to gravity || Acceleration due to gravity below the surface of earth || Acceleration due to gravity above the surface of earth
Inertial and Gravitational Mass
Gravitational Potential Energy || Expression for Gravitational Potential Energy || Gravitational Potential
Planetary Motion || Kepler’s 1st law Vs. Copernicus Model || Kepler’s 2nd law: Law of Areas || Kepler’s 3rdLaw: Law of periods
Escape Velocity || Example of Escape Velocity: No atmosphere on moon || Earth Satellites || Natural Satellite || Artificial Satellites
Determining the Time Period of Earth Satellite || Energy of an orbiting satellite || Geostationary Satellite || Polar Satellites || Weightlessness
NCERT Solutions for Class 11 Physics Chapter 8 Gravitation
Class 11 Physics Chapter 9 mechanics properties of solid
Section Name Topic Name 9 Mechanical Properties Of Solids 9.1 Introduction 9.2 Elastic behaviour of solids 9.3 Stress and strain 9.4 Hooke’s law 9.5 Stress-strain curve 9.6 Elastic moduli 9.7 Applications of elastic behaviour of materials
0/6
Introduction || Solids and their mechanical properties
16:02
Stress || Types of Stress
Strain || Types of Strain
Hook’s Law || Stress – Strain Curve || Elastic Modulus || Types of Elastic Modulus
Compressibility
NCERT Solutions for Class 11 Physics Chapter 9 Mechanical Properties of Solids
Class 11 Physics Chapter 10 Mechanical Properties of Fluids
Section Name Topic Name 10 Mechanical Properties Of Fluids 10.1 Introduction 10.2 Pressure 10.3 Streamline flow 10.4 Bernoulli’s principle 10.5 Viscosity 10.6 Reynolds number 10.7 Surface tension
0/11
Introduction:Fluids || Pressure
16:21
Pressure in Fluids || Pascal’s Law
Variation of pressure with depth || Hydrostatic Paradox
Atmospheric Pressure || How to measure atmospheric pressure? || Gauge Pressure || How to measure Gauge pressure || Absolute Pressure
Pascal’s law for transmission of fluid pressure|| Application of Pascal’s Law || Types of Fluid flow: Steady Flow || Equation of Continuity || Turbulent Flow
Bernoulli’s Principle || Torricelli’s law || Derivation of the Law
Venturimeter || Practical Application of Venturimeter || Dynamic Lift || Magnus Effect
Viscosity || Coefficient of Viscosity || Stokes Law || Terminal Velocity
Reynolds Number || Turbulence:boon or bane || Liquid Surfaces || Surface Energy || Surface energy for two fluids in contact
Surface Tension || How detergents work? || Angle of Contact || Significance of Angle of Contact || Drops and Bubbles || Pressure inside a drop and a cavity || Capillary Rise
NCERT Solutions for Class 11 Physics Chapter 10 Mechanical Properties of Fluids
Class 11 Physics Chapter 11 Thermal Properties of matter
Section Name Topic Name 11 Thermal Properties of matter 11.1 Introduction 11.2 Temperature and heat 11.3 Measurement of temperature 11.4 Ideal-gas equation and absolute temperature 11.5 Thermal expansion 11.6 Specific heat capacity 11.7 Calorimetry 11.8 Change of state 11.9 Heat transfer 11.10 Newton’s law of cooling
0/5
Introduction || Temperature and Heat || Relation between Joule and Calorie || Measurement of Temperature
19:31
Ideal-gas Equation and Absolute Temperature || Thermal Expansion || Types of Thermal Expansion
Anomalous Behaviour of Water || Thermal Stress || Heat Capacity || Molar specific heat capacity
Calorimetry || Change of State || Regelation || Vaporisation || Sublimation
NCERT Solutions for Class 11 Physics Chapter 11 Thermal Properties of matter
Class 11 Physics Chapter 12 Thermodynamics
Section Name Topic Name 12 Thermodynamics 12.1 Introduction 12.2 Thermal equilibrium 12.3 Zeroth law of thermodynamics 12.4 Heat, internal energy and work 12.5 First law of thermodynamics 12.6 Specific heat capacity 12.7 Thermodynamic state variables and equation of state 12.8 Thermodynamic processes 12.9 Heat engines 12.10 Refrigerators and heat pumps 12.11 Second law of thermodynamics 12.12 Reversible and irreversible processes 12.13 Carnot engine
0/7
Introduction || Thermodynamics vs. Mechanics || Thermal Equilibrium || Types of Equilibrium
19:58
System and Surroundings || Types of Systems || Types of Walls
Zeroth Law of Thermodynamics || Thermodynamic state variables || Types of thermodynamic state variables || Heat || Work || Internal Energy
First Law of Thermodynamics || Specific heat capacity || Specific heat capacity of water || Molar Specific Heat Capacity
Thermodynamic processes – Quasi Static Process || Isothermal Processes || Adiabatic Processes || Isochoric Processes || Isobaric Processes || Heat Engine
Refrigerator || Coefficient of Performance (COP) of the refrigerator || Second law of Thermodynamics || Reversible and Irreversible processes || Carnot engine
NCERT Solutions for Class 11 Physics Chapter 12 Thermodynamics
Class 11 Physics Chapter 13 Kinetic Theory
Section Name Topic Name 13 Kinetic Theory 13.1 Introduction 13.2 Molecular nature of matter 13.3 Behaviour of gases 13.4 Kinetic theory of an ideal gas 13.5 Law of equipartition of energy 13.6 Specific heat capacity 13.7 Mean free path
0/7
Introduction || Molecular nature of matter || John Dalton || Why was Dalton’s theory a success? || Behaviour of Gases || Justification of the Avogadro’s hypothesis from equation of gas
17:44
Perfect Gas Equation || Different Forms of Perfect Gas Equation || Ideal Gas || Real gases deviation from ideal gas
Deducing Dalton’s Law of partial pressures || To show how perfect gas equation concludes Dalton’s law of partial pressure || Kinetic Theory of an Ideal Gas || Law of Equipartition of energy:Degrees of Freedom
Translational degree of freedom || Rotational Degree of freedom || Vibrational degree of freedom
Law of Equipartition of energy || Specific Heat Capacity for monoatomic gases || Specific Heat of Diatomic gases (rigid) || Specific Heat of Diatomic gases (non-rigid) || Specific Heat Capacity for polyatomic gases || Specific Heat Capacity for solids || Specific Heat Capacity of water
Mean free path || Expression for mean free path
NCERT Solutions for Class 11 Physics Chapter 13 Kinetic Theory
Class 11 Physics Chapter 14 Oscillations
Section Name Topic Name 14 Oscillations 14.1 Introduction 14.2 Periodic and oscilatory motions 14.3 Simple harmonic motion 14.4 Simple harmonic motion and uniform circular motion 14.5 Velocity and acceleration in simple harmonic motion 14.6 Force law for simple harmonic motion 14.7 Energy in simple harmonic motion 14.8 Some systems executing Simple Harmonic Motion 14.9 Damped simple harmonic motion 14.10 Forced oscillations and resonance
0/5
Introduction || Periodic and Oscillatory motions || Displacement as a combination of sine and cosine functions || SHM || Angular Frequency
20:02
SHM & Uniform Circular Motion || Velocity in Simple Harmonic Motion || Acceleration in Simple Harmonic Motion
Energy in SHM || Oscillations due to spring
Simple Pendulum || DAMPED SIMPLE HARMONIC MOTION || Damping Force
NCERT Solutions for Class 11 Physics Chapter 14 Oscillations
Class 11 Physics Chapter 15 Waves
Section Name Topic Name 15 Waves 15.1 Introduction 15.2 Transverse and longitudinal waves 15.3 Displacement relation in a progressive wave 15.4 The speed of a travelling wave 15.5 The principle of superposition of waves 15.6 Reflection of waves 15.7 Beats 15.8 Doppler effect
0/8
Introduction || What is a wave? || Types of Waves
20:54
Displacement in a progressive wave || Amplitude and Phase of a wave || Expression of Phase || Wavelength || Wave Number || Time Period, Frequency and Angular frequency || Travelling Waves || The speed of a travelling wave
Different Expressions for Wave Speed || Dimensional Analysis to show how the speed is related to mass per unit length and Tension || Speed of a longitudinal wave in a stretched string || Dimensional Analysis to show how the speed is related to density and bulk modulus
The principle of superposition of waves || Reflection of Waves || Reflection at rigid boundary || Standing (Stationary) Waves || Difference between the travelling wave and stationary wave
Nodes and Antinodes of Standing Wave || Nodes || Nodes and Antinodes: system closed at both ends
Modes of Oscillations || Nodes and Antinodes: system closed at one end || Modes of oscillations
Beats || Beat Frequency || Doppler’s Effect
NCERT Solutions for Class 11 Physics Chapter 15 Waves
Class 11th Physics Online Class For 100% Result
About Lesson

Conservative & Non-Conservative Forces

  • Conservative forces are those for which work done depends only on initial and final points.
    Example- Gravitational force, Electrostatic force.
  • Non-Conservative forces are those where the work done or the kinetic energy did depend on other factors such as the velocity or the particular path taken by the object.
    Example- Frictional force.
Class 11 Physics Work Energy Power Notes
Work Energy Power

The Conservation of Mechanical Energy

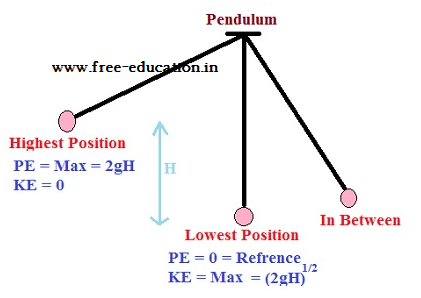
  • Mechanical Energy is the energy associated with the motion and position of an object.
  • The quantity K +V(x), is called the total mechanical energy of the system.
  • For a conservative force, ΔK = ΔW = F(x) Δx
    Also, – V(x) = F(x) Δx
  • This employs Δ(K+V) =0 for a conservative force.
  • Individually the kinetic energy K and the potential energy V(x) may vary from point to point, but the sum is a constant.
  • Conservative Force:
  • A force F(x) is conservative if it can be derived from a scalar quantity V(x) by the relation  : F(x) = – dv/dx
  • The work done by the conservative force depends only on the end points.
  • A third definition states that the work done by this force in a closed path is zero.
  • The total mechanical energy of a system is conserved if the forces, doing work on it, are conservative.
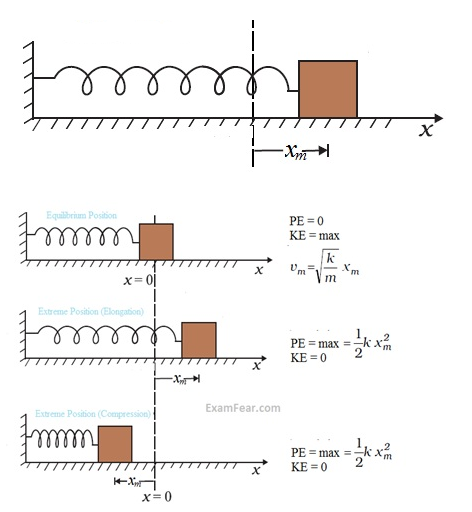
Class 11 Physics Work Energy Power Notes

Potential energy of spring

  • The spring force is an example of a variable force, which is conservative.
  • In an ideal spring, Fs = − kx , this force law for the spring is called Hooke’s law.
  • The constant k is called the spring constant. Its unit is N m-1.
  • The spring is said to be stiff if k is large and soft if k is small.
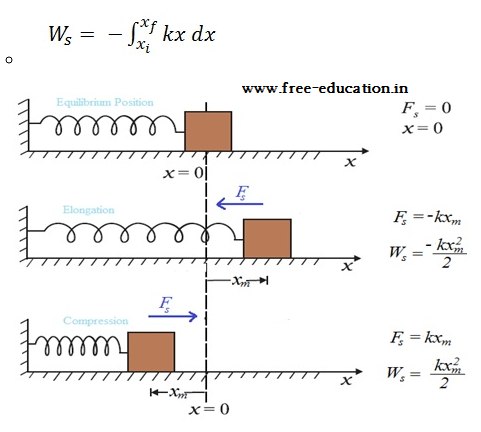
Class 11 Physics Work Energy Power Notes
Work Energy Power
  • Spring force is position dependent as first stated by Hooke, (Fs = − kx)
  • Work done by spring force only depends on the initial and final positions. Thus, the spring force is a conservative force.
  • We define the potential energy V(x) of the spring to be zero when block and spring system is in the equilibrium position.
  • For an extension (or compression) x,  V(x) = kx2/2

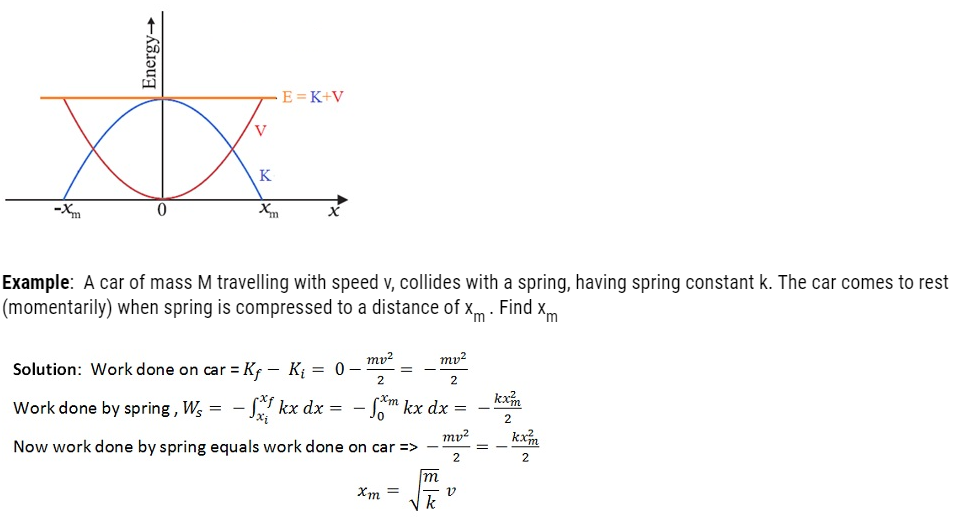
If the block of mass m is extended to xm and released from rest, then its total mechanical energy at any arbitrary point x (where x lies between – xm and + xm) will be given by:

Class 11 Physics Work Energy Power Notes
Previous
Next
Wisdom TechSavvy Academy