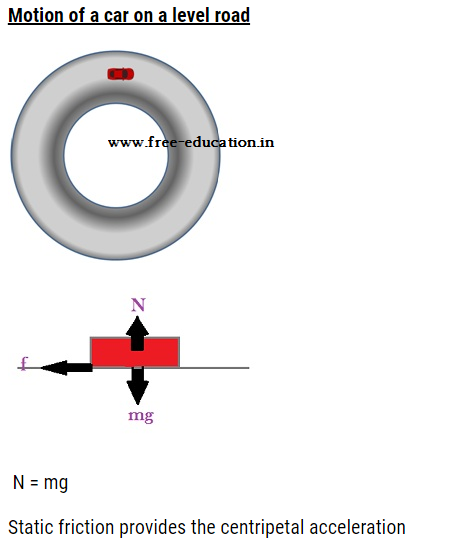
f_s =< μ_sN 

mv²/r  =< μ_sN   

v²  =< μ_sNR/m = μ_smgR/m = μ_sRg

v  =<  √ μ_sRg

This is the maximum speed of a car in circular motion on a level road.

In the vertical direction (Y axis)

Ncosϴ = fsinϴ + mg ——————–(i)

In horizontal direction (X axis)

fcosϴ + Nsinϴ = mv²/r  —————-(ii)

Since we know that f      μ_sN   

For maximum velocity, f = μ_sN

(i)becomes:

       Ncosϴ = μ_sNsinϴ + mg

Or, Ncosϴ – μ_sNsinϴ = mg

Or, N = mg/(cosϴ- μ_ssinϴ)

Put the above value of N in (ii)

μ_sNcosϴ + Nsinϴ = mv²/r 

μ_smgcosϴ/(cosϴ- μ_ssinϴ) + mgsinϴ/(cosϴ- μ_ssinϴ) = mv²/r 

mg (sinϴ + μ_scosϴ)/ (cosϴ – μ_ssinϴ) = mv²/r 

Divide the Numerator & Denominator by cosϴ, we get

v² = Rg (tanϴ +μ_s) /(1- μ_s tanϴ)

v = √ Rg (tanϴ +μ_s) /(1- μ_s tanϴ)

This is the miximum speed of a car on a banked road.

Special case:

When the velocity of the car = v₀ ,

• No f is needed to provide the centripetal force. (μ_s =0)
• Little wear & tear of tyres take place.

             v_o = √ Rg (tanϴ)

 Problem: A circular racetrack of radius 300 m is banked at an angle of 15°. If the coefficient of friction between the wheels of a race-car and the road is 0.2, what is the

 (a) optimum speed of the racecar to avoid wear and tear on its tyres, and

(b) maximum permissible speed to avoid slipping ?

 Solution.

R = 300m

ϴ = 15^o

μ_s  = 0.2

• v_o = √ Rg tanϴ

      = √300 * 9.8 * tan 15^o

      = 28.1 m/s

• v_max = √ Rg (tanϴ +μ_s) /(1- μ_s tanϴ)

             = √ 300 * 9.8 * (0.2 + tan 15^o)/(1-0.2tan15^o)

             = 38.1 m/s