Thermodynamic processes – Quasi Static Process
- Quasi static term means semi static .It is not purely moving.
- It is a hypothetical construct which means it is not in real.
- It is an infinitely slow process which means change from its original position is not at all significant.
- System changes its variables (P, T, and V) so slowly that it remains in equilibrium with its surroundings throughout.
- Consider a gas initially at Pressure (P) and Temperature (T) changes it to a new state whose Pressure is (P’) and Temperature (T’).
- If we change the surrounding pressure to P by very small amount then allow the system to reach that system.
- The characteristics for a system to be Quasi-static process
- Extremely very slow process.
- There should not be any accelerated motion. Not large temperature gradient. Temperature gradient means the

In a quasi-static process, the temperature of the surrounding reservoir and the external pressure differ only infinitesimally from the temperature and pressure of the system.
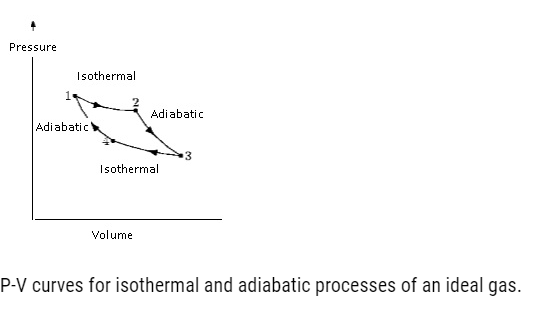
Isothermal Processes
- Isothermal: – Iso means same and thermal related to temperature. In Isothermal process the temperature remains constant throughout while all other variables change.
- Temperature is constant throughout.
- For an ideal gas
- PV = nRT where
- n=no. of moles (constant), R = universal gas constant, T =constant for isothermal process.
- This implies PV=constant
- Pressure and volume are inversely proportional to each other.
- Graphically if we plot pressure and volume



Adiabatic Processes
- Adiabatic is a process in which there is no heat flow takes place between the system and the surroundings.
- These processes are sudden.
- The walls of the container should be adiabatic
- For an adiabatic process of an ideal gas
- From Boyle’s law
- PV γ = constant
Where γ = Cp/Cv Specific heat ratio
Example: – Hot tea in Thermos flask. It will remain hot as there is no exchange of heat takes place because the walls of thermos is insulating.
Problem: – A cylinder with a movable piston contains 3 moles of hydrogen at standard temperature and pressure. The walls of the cylinder are made of a heat insulator, and the piston is insulated by having a pile of sand on it. By what factor does the pressure of the gas increase if the gas is compressed to half its original volume?
Answer: The cylinder is completely insulated from its surroundings. As a result, no heat is exchanged between the system (cylinder) and its surroundings. Thus, the process is adiabatic.
Initial pressure inside the cylinder = P1
Final pressure inside the cylinder = P2
Initial volume inside the cylinder = V1
Final volume inside the cylinder = V2
Ratio of specific heats, γ = 1.4
For an adiabatic process, we have: P1V1 γ = P2V2 γ
The final volume is compressed to half of its initial volume.
V2= V1/2
P1V1 γ = P2 (V1/2) γ
=P2/P1 = V1 γ/ ( V1/2) γ = (2) γ = (2)1.4 =2.639
Hence, the pressure increases by a factor of 2.639.
Graphically if we plot pressure and volume.
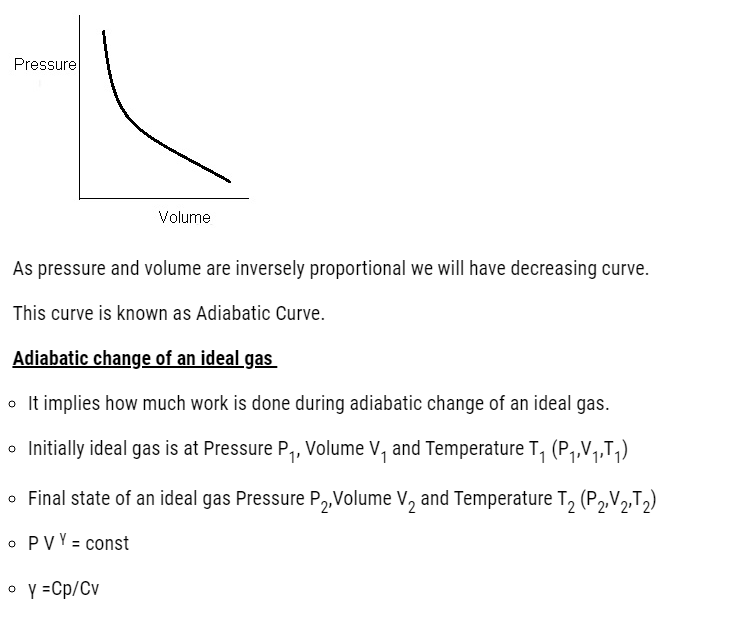
- If an ideal gas undergoes a change in its state adiabatically from (P1, V1) to (P2, V2)
- P1V1 γ = P2V2 γ
- The work done in an adiabatic change of an ideal gas from the
state (P1, V1, T1) to the state (P2, V2, T2).
W =∫ P V dV = P ∫V dV (Integrating between the limits V2 and V1)
For Adiabatic Process
- P V γ = constant This implies P= constant / V γ
- W = constant ∫dV/ V γ
- constant [V γ-1/- γ+1]
- constant/1- γ [V21- γ – V1 1-γ]
- = constant/1- γ[1/ V21- γ– 1/ V1 1-γ]
- By solving Work done W= R/ (γ-1)(T2-T1), where
- T2= final Temperature
- T1=initial temperature
- R=Universal gas constant
- γ = Specific heat ratio
- This is the work done during adiabatic change.
- Consider W= R/ (γ-1)(T2-T1)
Case 1: W>0 (when T1>T2)
Temperature of the gas decreases.
Case 2:- W< 0 (T1<T2)
Temperature of the gas increases.
Isochoric Processes
- Isochoric process means volume is constant while all other variables change.
- As volume is kept constant therefore no work is done on or by the gas.
- Heat absorbed by the gas is completely used to change its internal energy and its temperature.
- From First law of Thermodynamics
- ΔQ= Δ U + ΔW (ΔW =0)
- ΔQ= Δ U
- This means whatever heat is supplied to the system that is used up completely to change the internal energy and temperature of the system.
- Cv = Δ U/ Δ T
Example: – If we heat a gas filled in a closed cylinder fitted with a piston. When we supply heat to this cylinder the piston won’t move as there is as there is no volume change. There will be no work is also being done. Whatever the heat is added it will be used to increase the internal energy of the system.

Isobaric Processes
- Iso means same and baric is related to pressure.
- In this process pressure is constant while all other variables change.
- Process in which pressure is constant.
- Work done is given as :
- W=P (V2-V1)
- =μ R (T2 – T1)
- From First law of thermodynamics
- ΔQ= Δ U + ΔW
- ΔQ= Δ U + μ R (T2 – T1)
- We can see from the above equation that the heat absorbed goes partly to increase internal energy and partly to do work.
Example: –
- Consider a cylinder filled with gas fitted with piston. When we heat the cylinder the gas expands but the pressure remains the same because of piston.
- Boiling water in an open pot which is at atmospheric pressure. When the water boils it changes to steam and this steam expands and since it is not contained, it stays at atmospheric pressure. So the pressure remains constant but energy changes.



Its volume is then reduced to the original value from E to F by an isobaric process. Calculate the total work done by the gas from D to E to F?
Answer:
Total work done by the gas from D to E to F = Area of ΔDEF
Area of ΔDEF = ½ x DE x EF
Where,
DF = Change in pressure = 600 N/m2
– 300 N/m2
= 300 N/m2
FE = Change in volume
= 5.0 m3
– 2.0 m3
= 3.0 m3
Area of ΔDEF =1/2x300x3 = 450 J
Therefore, the total work done by the gas from D to E to F is 450 J.

Consider a hot reservoir having a temperature T1 and a cold reservoir having a temperature T2.
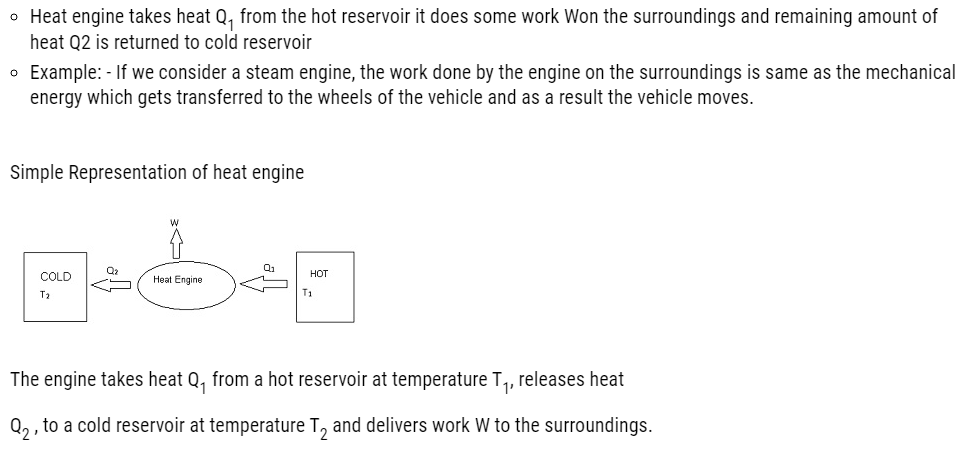
Efficiency of a heat engine:
- Efficiency indicates how much useful work we get as an output by the engine by using the amount of heat energy as input.
- It is denoted by η.
- Mathematically :
- η = W/Q1
- where W= output and Q1 = input
- By calculating
- η = 1- Q2/Q1
Where
- Q1=heat input in 1 cycle
- Q2=work done in 1 cycle.
- η = 1 – Q2/Q1
- For 100% efficient η = 1 ( which means Q2/Q1=0)
- There is always some heat is lost to the surroundings
- Heat lost (Q2) = 0
There is no heat engine whose efficiency is 100%.There is always some of the losses associated with the heat engines.
Problem: A steam engine delivers 5.4×108 J of work per minute and services 3.6 × 109 J of heat per minute from its boiler. What is the efficiency of the engine? How much heat is wasted per minute?
Answer:
Work done by the steam engine per minute, W = 5.4 × 108 J
Heat supplied from the boiler, H = 3.6 × 109 J
Efficiency of the engine =Output energy/Input energy
η = W/H = 5.4 x 108/ 3.6 × 109 = 0.15
Hence, the percentage efficiency of the engine is 15 %.
Amount of heat wasted = 3.6 × 109 – 5.4 × 108
= 30.6 × 108 = 3.06 × 109 J
Therefore, the amount of heat wasted per minute is 3.06 × 109 J.