Translational degree of freedom:-

• Translation means motion of the body as a whole from one point to another.

• For example:
  • Consider the oxygen molecule;it has 2 oxygen atoms which are bonded together.
  • The 2 oxygen atoms along with the bond are considered as whole body.
  • When the body as a whole is moving from one point to another is known as translational.
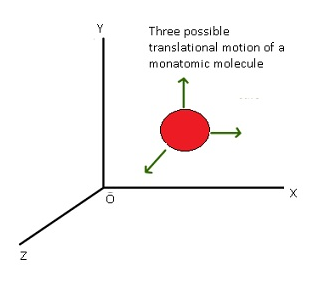
  • Consider a molecule which is free to move in space and so it will need 3 coordinates(x, y, z) to specify its location.
  • Therefore it has 3 degrees of freedom.
  • Similarly a molecule which is free to move in a plane which is 2 dimensional and so it needs 2 coordinates to specify its location.
  • Therefore it has 2 degrees of freedom.
  • Similarly a molecule which is free to move in line it needs 1 coordinate to specify its location.
  • Therefore it has 1 degree of freedom.
• Molecules of monoatomic gas have only translational degrees of freedom.This means gases which have only one atom.
• For example:-Helium atom it consists of only one He atom.It will have translationaldegrees of freedom.
• Each translational degree of freedom contributes a term that contains square of some variable of motion.
  • The variable of motion means the velocity (v_x,v_y,v_z).
  • The term (1/2) mv_x² will contribute to energy.This is Kinetic energy which is involved with the motion of the molecule from one point to another.

In thermal equilibrium, the average of each such term is (1/2) k_BT.

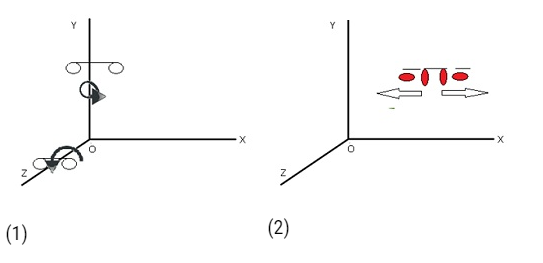
Rotational Degree of freedom

• Independent rotations that specify the orientation of a body or system.
  • There is rotation of one part of the body with respect to the other part.
• Rotational degree of freedom happens only in diatomic gas.
• Diatomic molecules have rotational degrees of freedom in addition to translational degrees of freedom.
• It is possible in diatomic molecules as 2 atoms are connected together by a bond.So the rotation of one atomw.r.t to other atom.
• In diatomic there is translational in addition to that they have rotational degree of freedom also.
  • For example: – Two oxygen atoms joined together by a bond. There are two perpendicular axes.
  • There are 2 rotations possible along the two axes.
  • They have 3 translational degrees of freedom and also 2 rotational degree of rotation.

• Therefore Rotational degree of freedom contributes a term to the energy that contains square of a rotational variable of motion.
• Rotational variable of motion comes from angular momentum ω.
  • Linear velocity is v_x,v_y,v_z. Whereas angular velocity is w_x,w_y,w_z.
  • E_R(rotational) = (1/2)(I₁ω₁)+(1/2)I₂ ω₂. These are 3 rotationaldegrees of freedom along the 2 perpendicular axes.
• The total energy contribution due to the degrees of freedom for oxygen molecule.
  • There will be 3 translational degree of freedom (1/2)m_xv_x²,(1/2)m_yv_y²,(1/2)m_zv_z²)
  • 2 rotational degree of freedom (1/2)I₁²ω₁²,(1/2)I₂²ω₂²

Vibrational degree of freedom

• Some molecules have a mode of vibration,i.e. its atoms oscillate along the inter-atomic axis like a one-dimensional oscillator.
• This vibration is observed in some molecules.
  • For example:- CO atoms oscillate along the interatomic axis like a

one-dimensional oscillator.

• Consider two 2 atoms they vibrate along the inter-atomic axis.
• The vibrational energy terms contain square of vibrational variables of motion.
• Total vibrational energy term E_v = (1/2) m (dy/dt)²+ (1/2) ky² where

 (1/2) m(dy/dt)²=Kinetic energy and (1/2)ky² =Potential energy and k=force constant one-dimensional oscillator.

• The vibrational degree of freedom contributes 2 terms.