Unit and Measurement NCERT Solution

Class 11th Physics Online Class For 100% Result

About Lesson

NCERT Exercises

Question 1. ( Unit and Measurements )
Fill in the blanks
(a) The volume of a cube of side 1 cm is equal to ….m³.
(b) The surface area of a solid cylinder of radius 2.0 cm and height 10 cm is equal to ….(mm)².
(c) A vehicle moving with a speed of 18 km h^-1… m in 1 s.
(d) The relative density of lead is 11.3. Its density is ….g cm^-3 or …kg m^-3.
Answer:
(a) The volume of a cube of side 1 cm is
given by, V = (1 cm)³or V= (10^-2m)³ = Kb⁶ m³.
(b) The surface area of a solid cylinder of radius r and height h is given by :
A = Area of two caps + curved surface area
= 2πr² + 2πrh = 2πr(r + h)
here r = 2 cm = 20 mm, h = 10 cm = 100 mm

∴ density of lead = relative density of lead x density of water
= 11.3 x 1 g cm^-3 = 11.3 g cm^-3Also in S.I. system density of water = 10³ kg m^-3density of lead = 11.3 x 10³ kg m^-3= 1.13 x 10⁴ kg m^-3

Question 2. ( Unit and Measurements )
Fill in the blanks by suitable conversion of units
(a) 1 kg m² s^-2 = ….g cm² s^-2(b) 1 m =… ly
(c) 0 m s^-2 = …km h^-2(d) G = 6.67 x 10-¹¹ N m² (kg)^-2 =…. (cm)³ s^-2Answer:
(a) 1 kg m²s^-2 = 1 x 10³ g (10² cm)² s^-2= 10⁷ g cm² s^-2

Question 3. ( Unit and Measurements )
A calorie is a unit of heat or energy and it equals about 4.2 J where 1 J = 1 kg m² s^-2. Suppose we employ a system of units in which the unit of mass equals α kg, the unit of length equals β m, the unit of time isϒ s. Show that a calorie has a magnitude 4.2 α^-1 β^-2 ϒ^-2 in terms of the new units

Question 4. ( Unit and Measurements )
Explain this statement clearly:
“To call a dimensional quantity’large’or’small’ is meaningless without specifying a standard for comparison”. In view of this, reframe the following statements wherever necessary:
(a) atoms are very small objects
(b) a jet plane moves with great speed
(c) the mass of Jupiter is very large
(d) the air inside this room contains a large number of molecules
(e) a proton is much more massive than an electron
(f) the speed of sound is much smaller than the speed of light.
Answer:
The given statement is correct. Measurement is basically a comparison process. Without specifying a standard of comparison, it is not possible to get an exact idea about the magnitude of a dimensional quantity. For example, the statement that the mass of the earth is very large, is meaningless. To correct it, we can say that the mass of the earth is large in comparison to any object lying on its surface.
(a) The size of an atom is much smaller than the sharp tip of a pin.
(b) A jet plane moves with a much larger speed than a superfast train.
(c) The mass of Jupiter is very large as compared to that earth.
(d) The air inside this room contains a very large number molecules as compared to that in a balloon.
(e) The given statement is correct.
(f) The given statement is correct.

Question 5. ( Unit and Measurements )
A new unit of length is chosen such that the speed of light in vacuum is unity. What is the distance between the Sun and the Earth in terms of the new unit if light takes 8 min and 20 s to cover this distance?
Answer:
According to problem, speed of light in vacuum, c = 1 new unit of length s^-1.
Time taken by light to cover distance between sun and the earth.
t = 8 min 20 s = 500 s.
∴ Distance between sun and earth
= c x t = 1 new unit of length x 500 s
= 500 new units of length

Question 6. ( Unit and Measurements )
Which of the following is the most precise device for measuring length :
(a) a vernier callipers with 20 divisions on the sliding scale
(b) a screw gauge of pitch 1 mm and 100 divisions on the circular scale
(c) an optical instrument that can measure length to within a wavelength of light?
Answer:Answer: (a) Least count of vernier callipers = 1/20 = 0.05 mm = 5 x 10^-5 m
(b) Least count of screw gauge =Pitch/No. of divisions on circular scale = 1 x 10^-3/100 = 1 x 10^-5 m
(c) Least count of optical instrument = 6000 A (average wavelength of visible light as 6000 A) = 6 x 10-⁷m As the least count of optical instrument is least, it is the most precise device out of three instruments given to us.
The most precise device is that whose least count is minimum.
Now:

Question 7. ( Unit and Measurements )
A student measures the thickness of a human hair by looking at it through a microscope of magnification 100. He makes 20 observations and finds that the average width of the hair in the field of view of the microscope is 3.5 mm. What is the estimate on the thickness of hair
Answer:Answer: As magnification, m =thickness of image of hair/ real thickness of hair = 100
and average width of the image of hair as seen by microscope = 3.5 mm
.•. Thickness of hair =3.5 mm/100 = 0.035 mm

Question 8. ( Unit and Measurements )
Answer the following:
(a) You are given a thread and a meter scale. How will you estimate the diameter of the thread?
(b) A screw gauge has a pitch of 1.0 mm and 200 divisions on the circular scale. Do you think it is possible to increase the accuracy of the screw gauge arbitrarily by increasing the number of divisions on the circular scale?
(c) The mean diameter of a thin brass rod is to be measured by vernier callipers. Why is a set of 100 measurements of the diameter expected to yield a more reliable estimate than a set of 5 measurements only?
Answer:
(a) The diameter of a thread is so small that it cannot be measured using a meter scale. We wind a number of turns of the thread on the meter scale so that the turns are closely touching one another. Measure the length (Z) of the windings on the scale which contains n number of turns
Diameter of thread =1/n
(b)

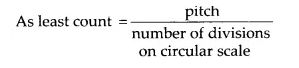
∴ theoretically speaking, least count decreases on increasing the number of divisions on the circular scale. Hence, accuracy would increase. Practically, it may not be possible to take the reading precisely due to low resolution of human eye.
(c) A large number of observations (say, 100) will give more reliable result than smaller number of observations (say, 5). This is because larger the number of readings, closer is the arithmetic mean to the true value and hence smaller the random error.

Question 9. ( Unit and Measurements )
The photograph of a house occupies an area of 1.75 cm² on a 35 mm slide. The slide is projected on to a screen, and the area of the house on the screen is 1.55 m². What is the linear magnification of the projector-screen arrangement.
Answer:

Question 10. ( Unit and Measurements )
State the number of significant figures in the following:
(a) 007 m²
(b) 2.64x 10²⁴kg
(c) 0.2370gem³
(d) 6.320J
(e) 032 Nm²
(f) 0.0006032 m²Answer:
(a) 0 .007 m² has one significant figures.
(b) 64 x 10²⁴ kg has three significant figures.
(c) 2370 g cm^-3 has four significant figures.
(d) 320 J has four significant figures.
(e) 032 N nr² has four significant figures.
(f) 0006032 m² has four significant figures.
(g) The length, breadth and thickness of a

Question 11. ( Unit and Measurements )
The length, breadth and thickness of a rectangular sheet of metal are 4.234 m, 1.005 m and 2.01 cm respectively. Give the area and volume of the sheet to correct significant figures.
Answer:
Given, length, (Z) = 4.234 m,
breadth (b) = 1.005 m
thickness, d = 2.01 cm = 2.01 x 10^-2 m
Area of sheet = 2 (lb + bd + dl)
= 2(4.234 x 1.005 +1.005 x 0.0201 + 0.0201 x 4.234)
= 2(4.3604739) = 8.7209478 m²As the least number of significant figure in thickness is 3. Therefore, area has 3 significant
figure, Area = 8.72 m²volume of metal sheet = Z x b x d
= 4.234 x 1.005 x 0.0201 m³ = 0.085528917 m³After rounding off = 0.0855 m³

Question 12. ( Unit and Measurements )
The mass of a box measured by a grocer’s balance is 2.300 kg. Two gold pieces of masses 20.15 g and 20.17 g are added to the box. What is (a) the total mass of the box, (b) the difference in the masses of the pieces to correct significant figures?
Answer:
Here, mass of the box, m = 2.3 kg
Mass of one gold piece,m₁= 20.15 g = 0.02015 kg
Mass of other gold piece, m₂ = 20.17 g = 0.02017 kg
(a) Total mass = m + m₁ + m₂= 2.3 + 0.02015 + 0.02017 = 2.34032 kg As the result is correct only upto one place of decimal, therefore, on rounding off total mass = 2.3 kg
(b) Difference in masses = m₂– m₁
= 20.17-20.15 = 0.02 g
(correct upto two places of decimal).

Question 13. ( Unit and Measurements )
A physical quantity P is related to four observables a, b, c and d as follows:
P = a³b²l (√c d)
The percentage errors of measurement in a, b, c and d are 1%, 3%, 4% and 2%, respectively. What is the percentage error in the quantity PI If the value of P calculated using the above relation turns out to be 3.763, to what value should you round off the result?

Question 14. ( Unit and Measurements )
A book with many printing errors contains four different formulas for the displacement y of a particle undergoing a certain periodic motion
(a) y = asin2πt/T
(b) y = asinvt
(c) y = (a/T) sin t/a
(d) y = (a√2) (sin2πt/T+ cos2πt/T)
(a = maximum displacement of the particle, v = speed of the particle. T = time-period of motion.)
Rule out the wrong formulas on dimensional grounds.”
Answer:
The argument of a trigonometrical function, i.e. angle is dimensionless. Now using the principle of homogeneity of dimensions.

Question 15.
Famous relation in physics relates ‘moving mass’ m to the ‘rest mass’ m_a of a particle in terms of its speed v and the speed of light, c. (This relation first arose as a consequence of special theory of relativity due to Albert Einstein). A boy recalls the relation almost correctly but forgets where to put the constant c. He writes:

Guess where to put the missing c.

Question 16.
The unit of length convenient on the atomic scale is known as an angstrom and is denoted by
A: 1 A = 10^-10 The size of a hydrogen atom is about 0.5 A. What is the total atomic volume in m³ of a mole of hydrogen atoms?
Answer:

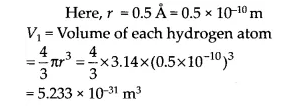
According to Avogadro’s hypothesis, one mole of hydrogen contains :
N = 6.023 x 10²³ atoms
∴ Atomic volume of 1 mole of hydrogen atoms,
V=NV1,
or V= 6.023 x 10²³ x 5.233 x 10^-3= 3.152 x 10-⁷m³ ≅ 3 x 10^-7 m³

Question 17.
One mole of an ideal gas at standard temperature and pressure occupies 22.4 L (molar volume). What is the ratio of molar volume to the atomic volume of a mole of hydrogen? (Take the size of hydrogen molecule to be about 1 Å). What is this ratio so large?
Answer:

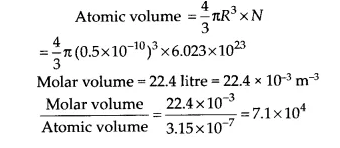
The large value of ratio shows that the inter molecular separation in a gas is much larger than the size of a molecule

Question 18.
Explain this common observation clearly: If you look out of the window of a fast moving train, the near by trees, houses etc. seem to move rapidly in a direction opposite to the train’s motion, but the distant objects (hill tops, the Moon, the stars etc.) seem to be stationary. (In fact, since you are aware that you are moving,, these distant objects seem to move with you).
Answer:
The line joining the object to the eye is called the line of sight. When a train moves rapidly, the line of sight of a nearby tree changes its direction of motion rapidly i.e. near objects make greater angle than distant objects. Therefore the trees appear to run in opposite direction.

On the other hand, the angular change i.e. the line of sight of far off objects (hill tops, the moon, the stars etc.) changes its direction extremely slowly and hence the relative shift in their position is negligible. Hence they appear to be stationary i.e. move in the direction of the train i.e. appear to move with the observer in the train.

Question 19.
The principle of ‘parallax’ is used in the determination of distances of very distant stars The baseline AB is the line joining the Earth’s two locations six months apart in its orbit around the Sun. That is, the baseline is about the diameter of the Earth’s orbit = 3 x 10¹¹ m. However, even the nearest stars are so distant that with such a long baseline, they show parallax only of the order of 1″ (second) of arc or so. A parsec is a convenient unit of length on the astronomical scale. It is the distance of an object that will show a parallax of 1″ (second) of arc from opposite ends of a baseline equal to the distance from the Earth to the Sun. How much is a parsec in terms of meters?
Answer:

Question 20.
The nearest star to our solar system is 4.29 light years away. How much is this distance in terms of parsecs? How much parallax would this star (named Alpha Centauri) show when viewed from two locations of the Earth six months apart in its orbit around the Sun?
Answer:
Distance = 4.29 light year
= 4.29 x 9.46 x 10¹⁵m
( 1 light year = 9.46 x 10^-5m)

Question 21.
Precise measurements of physical quantities are a need of science. For example, to ascertain the speed of an aircraft, one must have an accurate method to find its positions at closely separated instants of time. This was the actual motivation behind the discovery of radar in World War II. Think of different examples in modern science where precise measurements of length, time, mass etc, are needed. Also, wherever you can, give a quantitative idea of the precision needed.
Answer:
Some of the examples of modem science, where precise measurements play an important role, are as follows :

Electron microscope uses an electron beam of wavelength 0.2 A to study very minute objects like viruses, microbes and the crystal structure of solids.
The successful launching of artificial satellites has been made possible only due to the precise technique available for accurate measurement of time-intervals.
The precision with which the distances are measured in Michelson-Morley Interferometer helped in discarding the idea of hypothetical medium ether and in developing the Theory of Relativity by Einstein.

Question 22.
Just as precise measurements are necessary in science, it is equally important to be able I to make rough estimates of quantities using rudimentary ideas and common observations. Think of ways by which you can estimate the following (where an estimate is difficult to obtain, try to get an upper bound on the quantity):
(a) the total mass of rain-bearing clouds over India during the Monsoon
(b) the mass of an elephant
(c) the wind speed during a storm
(d) the number of strands of hair on your head
(e) the number of air molecules in your classroom.
Answer:
(a) During Monsoon in India, the average rain fall is about 100 cm i.e. 1 m over , the area of the country, which is about
A = 3.3 x 10⁶ km² = 3.3 x 10⁶ x 10⁶ = 3.3 x 10¹² m²Therefore, volume of the rain water,
V = A h = 3.3 x 10¹² x 1 = 3.3 x 10¹² m³Now, density of water, p = 10³ kg m^-3Hence, the total mass of rain-bearing clouds over India,
m = V ρ = 3.3 x 10¹² x 10³ = 3.3 x 10¹⁵ kg
(b) To estimate the mass of an elephant, consider a boat having base area A in a river. Mark a point on the boat upto which it is inside the water.
Now, move the elephant into the boat and again mark a point on the boat upto which it is inside the water. If h is the distance between the two marks, then
Volume of the water displaced by the elephant, V = Ah
According to Archimedes’ principle, mass of the elephant,
M = mass of the water displaced by the elephant
If ρ (= 10³ kg m^-3) density of the water, then M = Vρ= Ah ρ
(c) The wind speed during a storm can be found by measuring the angle of drift of an air balloon in a known time. Consider that an air balloon is at the point A at a vertical height h above the observation point O on the ground, when there is no wind Storm.
During the storm, suppose that the balloon moves to the point B in an extremely small time t as shown in figure.

(d) Let the area of the hair-bearing head be equal to A. With a fine micrometer, measure the thickness d (diameter) of the hair. Then, area of cross-section of the hair, a = π d²/4
If we ignore the interspacing between the hair, then the number of strands of hair on the head,

Question 23.
The Sun is a hot plasma (ionized matter) with its inner core at a temperature exceeding 10⁷ K, and its outer surface at a temperature of about 600 K. At these high temperatures, no substance remains in a solid or liquid phase. In what range do you expect the mass density of the Sun to be, in the range of densities of solids and liquids or gases? Check if your guess is correct from the following data:
mass of the Sun = 2.0 x 10³⁰ kg,
radius of the Sun = 7.0 x 10⁸ m.
Answer:

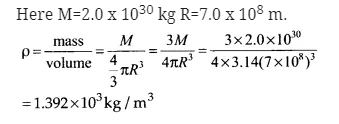
This is the order of density of solids and liquids; and not gases. The high density of sun is due to inward gravitational attraction on outer layers, due to the inner layers of the sun.

Question 24.
When the planet Jupiter is at a distance of 7 million kilometers from the Earth, its angular diameter is measured to be 35.72″ of arc. Calculate the diameter of Jupiter.

Question 25. ( Unit and Measurements )
A man walking briskly in rain with speed v must slant his umbrella forward making an angle 0 with the vertical. A student derives the following relation between 0 and v : tanθ = v and checks that the relation has a correct limit: as v —> 0,θ —> 0, as expected. (We are assuming there is no strong wind and that the rain falls vertically for a stationary man). Do you think this relation can be correct? If not, guess the correct relation.
Answer:
Here, given relation is tanθ = v No, this relation is not correct.
Since the left hand side of this relation is a trigonometrical function which is dimensionless, so R.H.S. must also be dimensionless. So v must
be $\frac { v }{ u }$ , where u = speed of rainfall. u
Hence, the correct relation becomes: v
tanθ = $\frac { v }{ u }$ u

Question 26. ( Unit and Measurements )
lt is claimed that two cesium clocks, if allowed to run for 100 years, free from any disturbance, may differ by only about 0.02 s. What does this imply for the accuracy of the standard cesium clock in measuring a time-interval of 1 s?
Answer:
Here, the difference shown by two clocks in 100 years = 0.02 s Therefore, the difference, the two clocks will show in 1s

Yes, both densities are of the same order of magnitude, i.e. of the order of 10³. This is because in the solid phase atoms are tightly packed.

Question 28. ( Unit and Measurements )
The unit of length convenient on the nuclear scale is a fermi: 1 f = 10-¹⁵m. Nuclear sizes obey roughly the following empirical relation:
r = r₀A^1/3where r is the radius of the nucleus, A its mass number, and r₀ is a constant equal to about, 1.2 f. Show that the rule implies that nuclear mass density is nearly constant for different nuclei. Estimate the mass density of sodium nucleus. Compare it with the average mass density of a sodium atom obtained in question 27.
Answer:
Let m be the average mass of a nucleon (neutron or proton).
As the nucleus contains A nucleons,
mass of nucleus M = mA
radius of nucleus r = r₀ A^1/3

As m and r₀ are constant, therefore, nuclear density is constant for all nuclei.
Using m = 1.66 x 10-²⁷ kg and

Question 29. ( Unit and Measurements )
A laser is a source of very intense, monochromatic, and unidirectional beam of light. These properties of a laser light can be exploited to measure long distances. The distance of the Moon from the Earth has been already determined very precisely using a laser as a source of light. A laser light beamed at the Moon takes 2.56 s to return after reflection at the Moon’s surface. How much is the radius of the lunar orbit around the Earth?
Answer:
Here, t = 2.56 s
velocity of laser light in vacuum,
c = 3 x 10⁸ m/s
The radius of lunar orbit is the distance of moon from earth. Let it be x

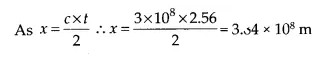
Question 30. ( Unit and Measurements )
A SONAR (sound navigation and ranging) uses ultrasonic waves to detect and locate objects under water. In a submarine equipped with a sonar the time delay between generation of a probe wave and the reception of its echo after reflection from an enemy submarine is found to be 77.0 s. What is the distance of the enemy submarine? (Speed of sound in water = 1450 m s¹).
Answer:

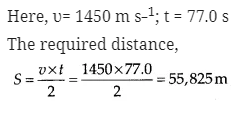
Question 31.( Unit and Measurements )

The farthest objects in our Universe discovered by modern astronomers are so distant that light emitted by them takes billions of years to reach the Earth. These objects (known as quasars) have many puzzling features, which have not yet been satisfactorily explained. What is the distance in km of a quasar from which light takes 3.0 billion years to reach us?
Answer:
Time taken, t = 3 x 10⁹ years
= 3 x 10⁹ x 365 x 24 – 60 x 60 s
Velocity of light, c = 3 x 10⁸ m s^_1Distance of quasar from earth = ct
= 3 x 10⁸ x 3 x 10⁹ x 365 x 24 x 3600 m
= 2.84 x 10²⁵ m = 2.84 x 10²² km.

Question 32. ( Unit and Measurements )
lt is a well known fact that during a total solar eclipse the disc of the moon almost completely covers the disc of the Sun. From this fact determine the approximate diameter of the moon.

Question 33. ( Unit and Measurements )
A great physicist of this century (P.A.M. Dirac) loved playing with numerical values of fundamental constants of nature. This led him to an interesting observation. Dirac found that from the basic constants of atomic physics (c, e, mass of electron, mass of proton) and the gravitational constant G, he could arrive at a number with the dimension of time. Further, it was a very large number, its magnitude being close to the present estimate on the age of the universe (=15 billion years). From the table of fundamental constants in the NCERT book, try to see if you too can construct this number (or any other interesting number you can think of). If its coincidence with the age of the universe were significant, what would this imply for the constancy of fundamental constants?
Answer:
The basic constants of atomic physics namely c-speed of light, e-charge on electron, m_c-mass of electron and m_p-mass of proton; and the gravitational constant G give rise to the quantity.