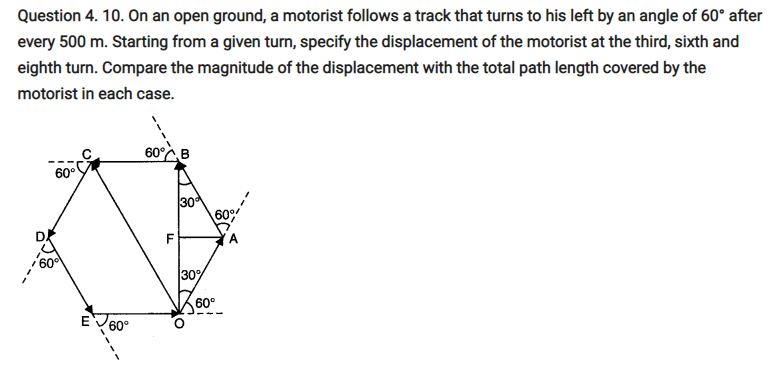
QUESTIONS FROM TEXTBOOK

Question 4. 1. State, for each of the following physical quantities, if it is a scalar or a vector: volume, mass, speed, acceleration, density, number of moles, velocity, angular frequency, displacement, angular velocity.
Answer:  Scalars: Volume, mass, speed, density, number of moles, angular frequency.
Vectors: Acceleration, velocity, displacement, angular velocity.

Question 4. 2. Pick out the two scalar quantities in the following list:
force, angular momentum, work, current, linear momentum, electric field, average velocity, magnetic moment, relative velocity.
Answer: Work and current are the scalar quantities in the, given list.

Question 4. 3. Pick out the only vector quantity in the following list:
Temperature, pressure, impulse, time, power, total path length, energy, gravitational potential, coefficient of friction, charge.
Answer:  Impulse.

Question 4. 4. State with reasons, whether the following algebraic operations with scalar and vector physical quantities are meaningful:
(a) adding any two scalars, (b) adding a scalar to a vector of the same dimensions, (c) multiplying any vector by any scalar, (d) multiplying any two scalars, (e) adding any two vectors, (f) adding a component of a vector to the same vector.
Answer: (a) No, because only the scalars of same dimensions can be added.
(b) No, because a scalar cannot be added to a vector.
(c) Yes, multiplying a vector with a scalar gives the scalar (number) times the vector quantity which makes sense and one gets a bigger vector. For example, when acceleration A is multiplied by mass m, we get a force F = ml
(d) Yes, two scalars multiplied yield a meaningful result, for example multiplication of rise in temperature of water and its mass gives the amount of heat absorbed by that mass of water.
(e) No, because the two vectors of same dimensions can be added.
(f) Yes, because both are vectors of the same dimensions.

Question 4.5. Read each statement below carefully and state with reasons, if it is true or false:
(a) The magnitude of a vector is always a scalar.
(b) Each component of a vector is always a scalar.
(c) The total path length is always equal to the magnitude of the displacement vector of a particle.
(d) The average speed of a particle (defined as total path length divided by the time taken to cover the path) is either greater or equal to the magnitude of average velocity of the particle over the same interval of time.
(e) Three vectors not lying in a plane can never add up to give a null vector.
Answer: (a) True, magnitude of the velocity of a body moving in a straight line may be equal to the speed of the body.
(b) False, each component of a vector is always a vector, not scalar.
(c) False, total path length can also be more than the magnitude of displacement vector of a particle.
(d) True, because the total path length is either greater than or equal to the magnitude of the displacement vector.
(e) True, this is because the resultant of two vectors will not lie in the plane of third vector and hence cannot cancel its effect to give null vector.

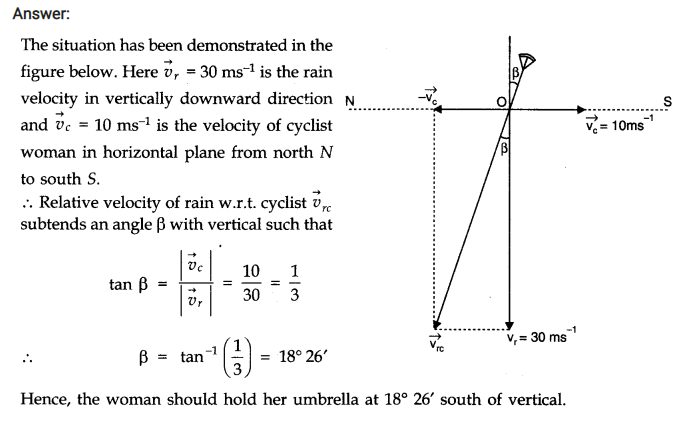
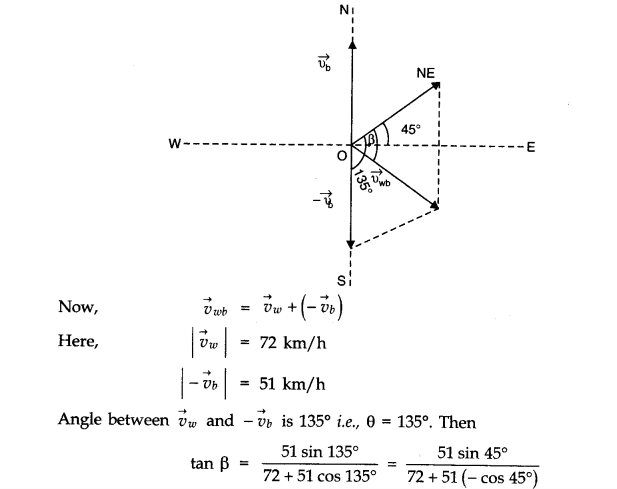
Question 4. 14. In a harbour, wind is blowing at the speed of 72 km/h and the flag on the mast of a boat anchored in the harbour flutters along the N-E direction. If the boat starts moving at a speed of 51 km/h to the north, what is the direction of the flag on the mast of the boat?
Answer:  When the boat is anchored in the harbour, the flag flutters along the N-E direction. It shows that the velocity of wind is along the north-east direction. When the boat starts moving, the flag will flutter along the direction of relative velocity of wind w.r.t. boat. Let V_wb be the relative velocity of wind w.r.t. boat and P be the angle between V_wb and vw (see fig. below)

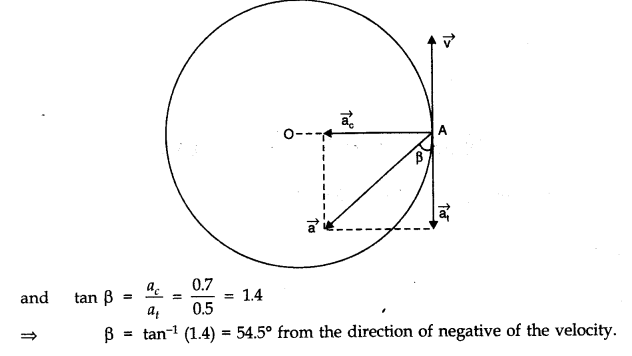
Answer: (a) False, the net acceleration of a particle in circular motion is along the radius of the circle towards the centre only in uniform circular motion.
(b) True, because while leaving the circular path, the particle moves tangentially to the circular path.
(c) True, the direction of acceleration vector in a uniform circular motion is directed towards the centre of circular path. It is constantly changing with time. The resultant of all these vectors will be a zero vector.

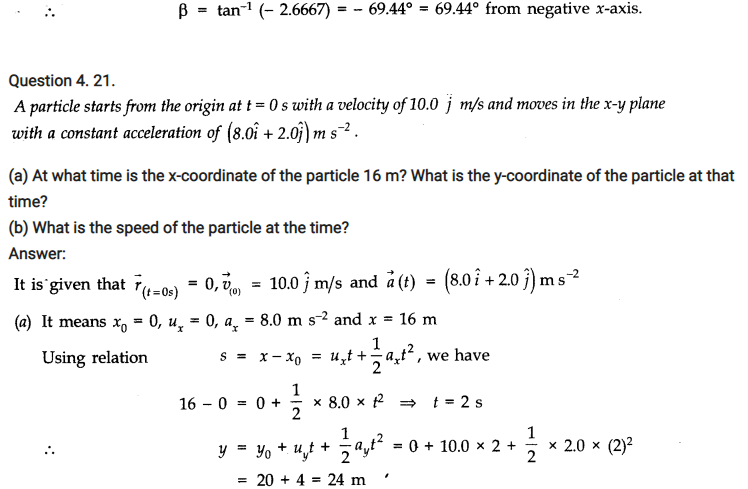
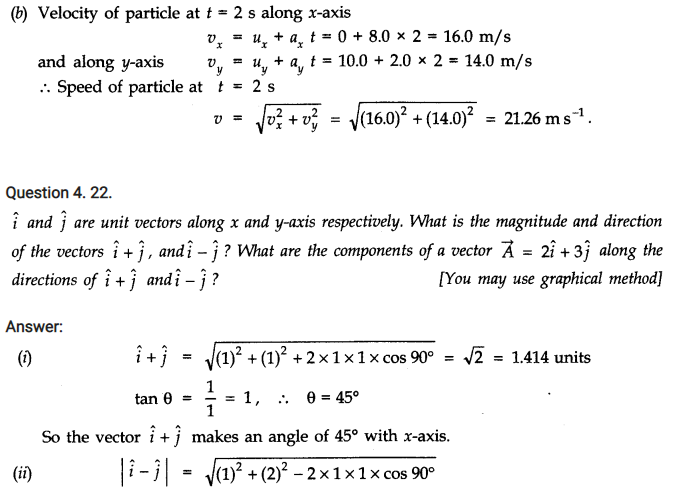
Answer: (b) and (e) are true; others are false because relations (a), (c) and (d) hold only for uniform acceleration.

Question 4. 24. Read each statement below carefully and state, with reasons and examples, if it is true or false: A scalar quantity is one that
(a) is conserved in a process
(b) can never take negative values
(c) must be dimensionless
(d) does not vary from one point to another in space
(e) has the same value for observers with different orientations of axes.
Answer: (a) False, because kinetic energy is a scalar but does not remain conserved in an inelastic collision.
(b) False, because potential energy in a gravitational field may have negative values.
(c) False, because mass, length, time, speed, work etc., all have dimensions.
(d) False, because speed, energy etc., vary from point to point in space.
(e) True, because a scalar quantity will have the same value for observers with different orientations of axes since a scalar has no direction of its own.

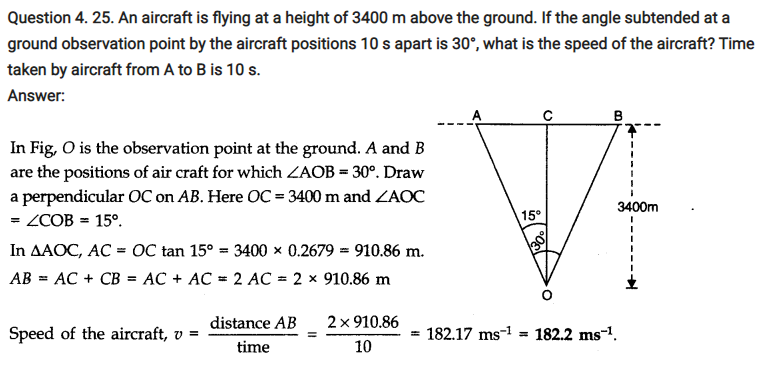
Question 4. 26. A vector has magnitude and direction.
(i) Does it have a location in the space?
(ii) Can it vary with time?
(iii) Will two equal vectors a and b at different locations in space necessarily have identical physical effects? Give examples in support of your answer.
Answer: (i) Besides having magnitude and direction, each vector has also a location in space.
(ii) A vector can vary with time. As an example, velocity and acceleration vectors may vary with time.
(iii) Two equal vectors a and b having different locations may not have same physical effect. As an example, two balls thrown with the same force, one from earth and the other from moon will attain different ‘maximum heights’.

Question 4. 27. A vector has both magnitude and direction. Does that mean anything that has magnitude and direction is necessarily a vector? The rotation of a body can be specified by the direction of the axis of rotation and the angle of rotation about the axis. Does that make any rotation a vector?
Answer:  No. Finite rotation of a body about an axis is not a vector because finite rotations do not obey the laws of vector addition.

Question 4. 28. Can you associate vectors with (a) the length of a wire bent into a loop (b) a plane area (c) a sphere? Explain.
Answer: (a) We cannot associate a vector with the length of a wire bent into a loop. This is because the length of the loop does not have a definite direction.
(b) We can associate a vector with a plane area. Such a vector is called area vector and its direction is represented by a normal drawn outward to the area.
(c) The area of a sphere does not point in any difinite direction. However, we can associate a null vector with the area of the sphere. We cannot associate a vector with the volume of a sphere.

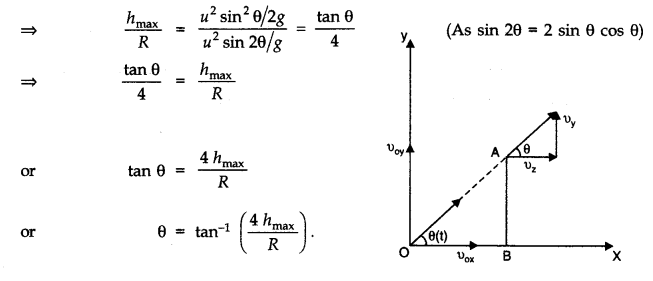
Question 4. 29. A bullet fired at an angle of 30° with the horizontal hits the ground 3 km away. By adjusting its angle of projection, can one hope to hit a target 5 km away? Assume the muzzle speed to the fixed, and neglect air resistance.
Answer:

Question 4. 31. A cyclist is riding with a speed of 27 km/h. As he approaches a circular turn on the road of radius 80 m, he applies brakes and reduces his speed at the constant rate of 0.50 m/s every second. What is the magnitude and direction of the net acceleration of the cyclist on the circular turn?
Answer: