Displacement in a progressive wave

• Amplitude and phase together describe the complete displacement of the wave.
• Displacement function is a periodic in space and time.
• Displacement of the particles in a medium takes place along the y-axis.
• Generally displacement is denoted as a function of X and T, but here it is denoted by y.
• In case of transverse wave displacement is given as:
• y(x,t) where x=propagation of the wave along x-axis, and particles oscillates along y-axis.
• Therefore y(x,t)= A sin(kx – ωt + φ).This is the expression for displacement.
• This expression is same as displacement equation which is used in oscillatory motion.
• As cosine function;y(x,t)= B cos(kx – ωt + φ),As both sine and cosine function)y (x, t) = A sin (kx – ωt + φ) + B cos(kx – ωt + φ)

Mathematically:

• Wave travelling along +X-axis: y(x, t) = a sin (kx – ωt + φ).
• Consider y=asin(kx – ωt + φ)=> y/a=sin(kx – ωt + φ)
• sin^-1(y/a) = kx-ωt =>kx=sin^-1(y/a) +ωt
• x=(1/k)sin^-1(y/a)+ (ωt/k)
• Wave travelling along –X-axis: x=(1/k)sin^-1(y/a)-(ωt/k)(only change in the sign ofωt)
• Conclusion:-
• As time t increases the value of x increases. This implies the x moves along x-axis.
• As time t decreases the value of x decrease. This implies the x moves along (-)ive x-axis.

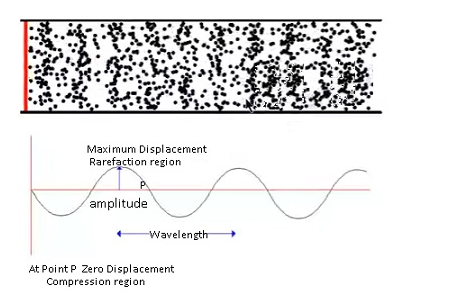
In case of longitudinal wave,

• There are regions of compressions (particles are closely packed) and rarefactions (particles are far apart).
• In compressions density of the wave medium is highest and in rarefactions density of the wave is lowest.
• Consider when the particle is at rarefaction, in that region as particle gets more space as a result the particles oscillates to the maximum displacement.
• Whereas in compressed region the particles oscillates very less as the space is not very much.
• The peak or the maximum amplitude is the centre of two compressed regions.Because at the centre of the two compressed region the particle is most free to displace to maximum displaced position.

Conclusion:-

• In case of longitudinal wave the particles will not oscillate to a very large distance. This displacement won’t represent the amplitude as it is not maximum possible displacement.

Amplitude is represented basically by the centre of the rarefaction region where the particle is most free to oscillate to its maximum displacement.

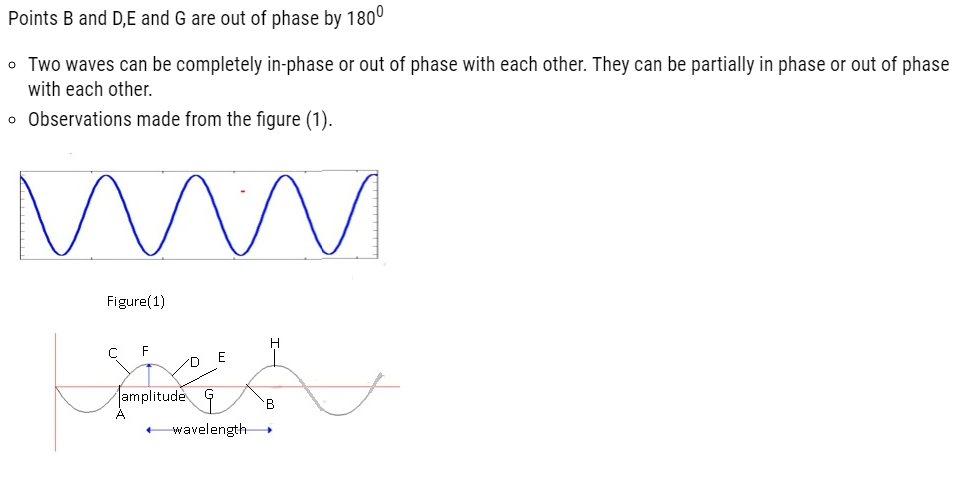
• Consider two points A and B on a wave.Their positions as well as their behaviour are same. Therefore points A and B are in phase.
• Consider points A and C on a wave. They are not in phase with each other as their position is not same.
• Similarly the points C and D are not in phase with each other as their positions are same but the behaviour is different. Thereforethey are not in phase with each other.
• Consider the points F and G their positions are same but the behaviour is totally opposite. So F and G are out of phase.
• Consider the points F and H;they are in phase with each other as their position is same as well as their behaviour.

Wavelength 

• The term wavelength means length of the wave.
• Wavelength is defined as the minimum distance between two consecutive points in the same phase of wave motion.
• It is denoted by λ.
• In case of transverse wave we use the term crest for thepeak of the maximum displacement.
• The point of minimum displacement is known as trough.
• In case of transverse wave wavelength is the distance between two consecutive crests or distance between two consecutive troughs.
• In case of longitudinal wave wavelength is the distance between the two compressions or the distance between the two rarefactions provided the compressions or rarefactions are nearest.

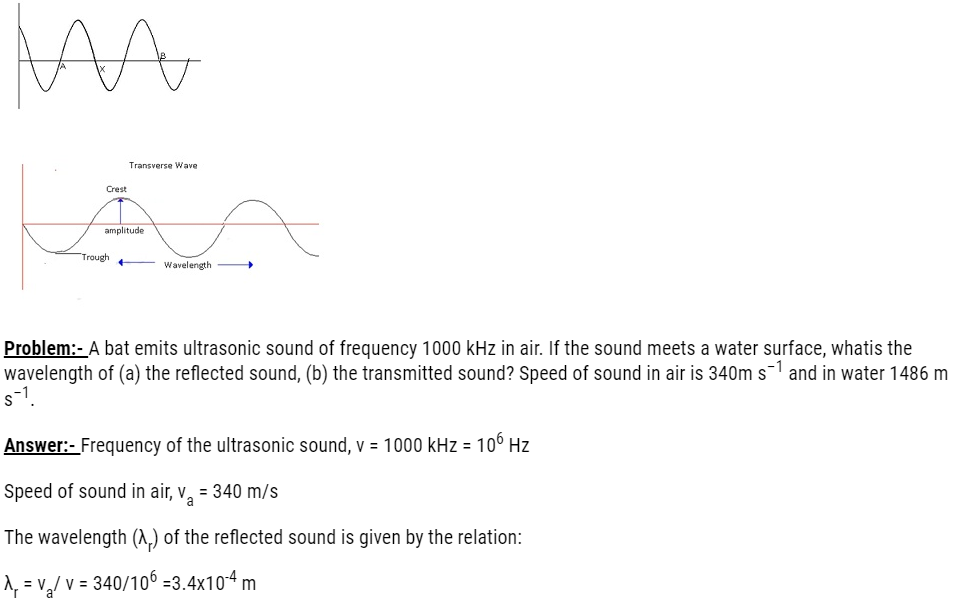
Frequency of the ultrasonic sound, ν = 1000 kHz = 10⁶ Hz

Speed of sound in water, v_w = 1486 m/s

The wavelength of the transmitted sound is given as:

λ_r = 1486/10⁶ =1.49 × 10^–3 m

Problem:- A hospital uses an ultrasonic scanner to locate tumours in a tissue. What is the wavelength of soundin the tissue in which the speed of sound is 1.7 km s^–1? The operating frequency of the scanner is4.2 MHz

Answer: Speed of sound in the tissue, v = 1.7 km/s = 1.7 × 10³ m/s.

Operatingfrequency of the scanner, ν = 4.2 MHz = 4.2 × 10⁶ Hz.

The wavelength ofsound in the tissue is given as:

λ=ν/v

= (1.7×10³)/ (4.2×10⁶)

=4.1×10^-4

Wave Number

Wave number describes the number of wavelengths per unit distance.

Denoted by ‘k’.

y(x,t)= a sin(kx – ωt + φ) assuming φ=0.

• At initial time t=0:-
  • y(x,0)=asin kx (i)
  • When x=x+λ then y(x+λ,0)=a sink(x+λ)   (ii)
  • When x=x+2λ then y(x+2λ,0)=a sink(x+2λ)

Value of y is equal at all points because all the points’ λ, 2λ are in phase with each other. Therefore,

From(i) and (ii) asin kx= a sink(x+λ)  =asin(kx+k λ)

This is true if and only if: -k λ =2 πn, where n=1, 2, 3…

k=(2 π n)/ λ. This is the expression for wave number.

k is also known as propagation constantbecause it tells about the propagationof the wave.

Wave number is an indirect way of describing the propagation of wave.

Time Period, Frequency and Angular frequency

1. Time Period of a wave: –
   1. Time Period of a wave is the time taken through one complete oscillation. It is denoted by’T’.
2. Frequency of a wave:-
   1. Frequency of a wave is defined as number of oscillations per unit time.It is denoted by ν.
   2. ν=1/T.
3. Angular frequency: –
   1. Angular frequency is defined as the frequency of the wave in terms of a circular motion.
   2. The term angular frequency is used only when there is an angle involved in the motion in that particular motion.
   3. It is denoted by ‘ω’.
   4. For example:-In linear motion angular frequency is not used but in case of wave the term angular frequency is used.

• Relation of with ω frequency ν is given ω= 2πνorω= 2π/T.

= 7.85 cm

(c) Now we relate T to ω by the relation

T = 2π/ω = (2 π)/ (3.0) s^–1

Frequency, v = 1/T = 0.48 Hz.

The displacement y at x = 30.0 cm andtime t = 20 s is given by

y = (0.005 m) sin (80.0 × 0.3 – 3.0 × 20)

= (0.005 m) sin (–36 + 12π)

= (0.005 m) sin (1.699)

= (0.005 m) sin (97⁰)

~ 5 mm

Problem:-

A transverse harmonic wave on a string is described by y(x,t) =3.0sin(36t+0.081x+(π/4))   Where x and y are in cm and t in s. The positive direction of x is from left to right. Is this a travelling wave or a stationary wave?

• If it is travelling, what are the speed and direction of its propagation?
• What are its amplitude and frequency?
• What is the initial phase at the origin?
• What is the least distance between two successive crests in the wave?

Answer:

• Yes; Speed = 20 m/s, Direction = Right to left
• 3 cm; 5.73 Hz,
• (π/4)
• 49 m

Explanation: The equation of a progressive wave travelling from right to left is given by the displacement

Function:y (x, t) = a sin (ωt + kx + Φ) … (i). The given equation is:

y(x, t) =3.0sin (36t+0.081x+(π/4))..(ii)

On comparing both the equations, we find that equation (ii) represents a travelling wave,

propagating fromright to left.

Now, using equations (i) and (ii), we can write:

ω = 36 rad/s and k = 0.018 m^–1. We knowthat:

ν=ω/ (2π) and λ= (2π)/k

Also, v = νλ

Therefore, ν=(ω/ (2π)) x (2π/k) = ω/k

=36/ (0.018)=2000cm/s=20m/s

Hence, the speed of the given travelling wave is 20 m/s.

Amplitude of the given wave, a = 3 cm

Frequency of thegiven wave:

ν=ω/ (2π) = 36/ (2×3.14) =5.73Hz

On comparing equations (i) and (ii), we find that the initial phase angle, Φ= (π/4)

The distance between two successive crests or troughs is equal to the wavelength of the wave.

Wavelength is given by the relation:

k=(2π)/λ

Therefore,

λ= (2π)/k = (2×3.14)/ (0.018) = 348.89cm=3.49m

The speed of a travelling wave

• To determine the speed of a travelling wave.
• The propagation of the wave always takes place along the +(ive) x-axis.
• It is denoted by v.
• Consider transverse wave moving along (+) ive x axis.
  • Displacement equation y (x, t) = a sin (kx – ωt) assuming φ=0.
• In case of transverse wave the y denotes the movement of particles along y-axis.x denotes the direction of wave propagation in terms of x axis.
• y-axis denotes the displacement of the particles of the medium in case of transverse wave and in case of longitudinal wavex denotes the movement of the particles along x-axis.
• In case of longitudinal wave the motion of particles takes place along x-axis and not along y-axis.
• The form of equation remains the same for both transverse and longitudinal wave.
• Only the direction of propagation i.e. the direction of the movement of the particles differs in case of transverse and longitudinal waves.
• We have considered only the motion along the horizontal direction i.e. x-axis. i.e. motion of all the peaks and which is a motion of a straight line.
• Displacement takes place along the straight line along x-axis.
• y component does not play much role as it talks about the movement of particles of the medium.
• When we are considering the peaks as a result phase does not have any role. That is phase is constant.
• y/a=sin(kx – ωt) => sin^-1 (y/a) = (kx- ωt )
  • => x=(1/k)sin^-1 (y/a) +ωt/k (where (1/k)sin^-1 (y/a)  is constant)
  • => Speed V=dx/dt =ω/k

(By differentiating with time,(1/k)sin^-1 (y/a) = 0 as differentiating a constant term is 0.) 

• Therefore Wave Speed V= ω/kwhereω=angular frequency and k=wave number.