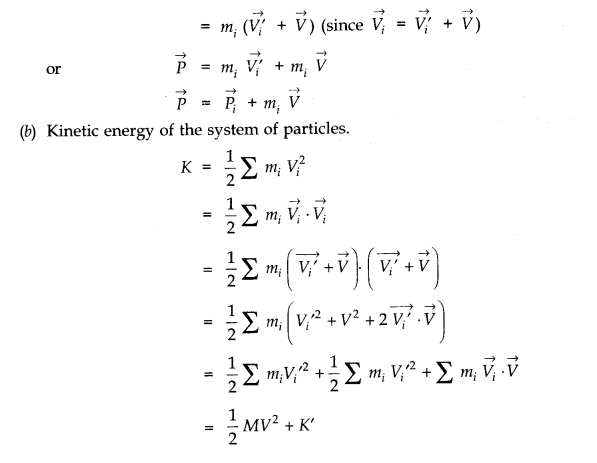QUESTIONS FROM TEXTBOOK
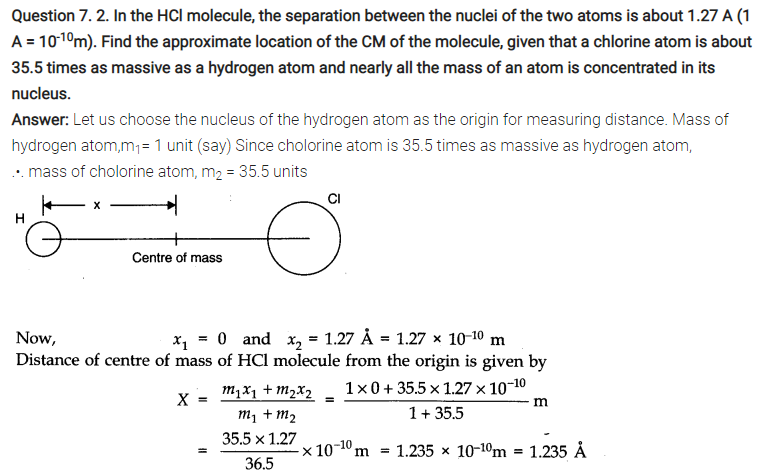
Question 7. 1. Give the location of the centre of mass of a (i) sphere, (ii) cylinder, (iii) ring, and (iv) cube, each of uniform mass density. Does the centre of mass of a body necessarily lie inside the body?
Answer: In all the four cases, as the mass density is uniform, centre of mass is located at their respective geometrical centres.
No, it is not necessary that the centre of mass of a body should lie on the body. For example, in case of a circular ring, centre of mass is at the centre of the ring, where there is no mass.
Question 7. 3. A child sits stationary at one end of a long trolley moving uniformly with a speed V on a smooth horizontal floor. If the child gets up and runs about on the trolley in any manner, what is the speed of the CM of the (trolley + child) system?
Answer: When the child gets up and runs about on the trolley, the speed of the centre of mass of the trolley and child remains unchanged irrespective of the manner of motion of child. It is because here child and trolley constitute one single system and forces involved are purely internal forces. As there is no external force, there is no change in momentum of the system and velocity remains unchanged.

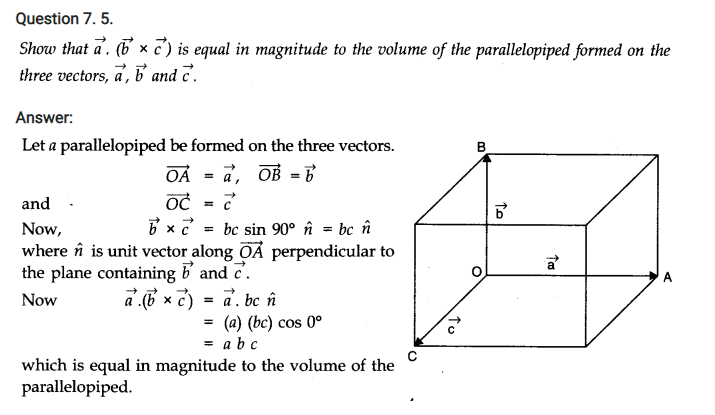






Question 7. 10. (a) Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be 2 MR2/5, where M is the mass of the sphere and R is the radius of the sphere.
(b) Given the moment of inertia of a disc of mass M and radius R about any of its diameters to 1 be 1/4 MR2, find the moment of inertia about an axis normal to the disc passing through a point on its edge.Applying theorem of parallel axes,Moment of inertia of sphere about a tangent to the sphere = 2/5 MR2 +M(R)2 =7/5 MR2
(b) We are given, moment of inertia of the disc about any of its diameters = 1/4 MR2
(i) Using theorem of perpendicular axes, moment of inertia of the disc about an axis passing through its centre and normal to the disc = 2 x 1/4 MR2 = 1/2 MR2.
(ii) Using theorem axes, moment of inertia of the disc passing through a point on its edge and normal to the dies = 1/2 MR2+ MR2 = 3/2 MR2.
Question 7. 11. Torques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. Which of the two will acquire a greater angular speed after a given time?
Answer: Let M be the mass and R the radius of the hollow cylinder, and also of the solid sphere. Their moments of inertia about the respective axes are I1 = MR2 and I2 = 2/5 MR2
Let τ be the magnitude of the torque applied to the cylinder and the sphere, producing angular accelerations α1and α2 respectively. Then τ=I1 α1 = I2 α2
The angular acceleration 04 produced in the sphere is larger. Hence, the sphere will acquire larger angular speed after a given time.
Question 7. 12. A solid cylinder of mass 20 kg rotates about its axis with angular speed 100 rad s-1. The radius of the cylinder is 0.25 m. What is the kinetic energy associated with the rotation of the cylinder? What is the magnitude of angular momentum of the cylinder about its axis?
Answer: M = 20 kg
Angular speed, w = 100 rad s-1; R = 0.25 m
Moment of inertia of the cylinder about its axis
=1/2 MR2 = 1/2 x 20 (0.25)2 kg m2 = 0.625 kg m2
Rotational kinetic energy,
Er = 1/2 Iw2 = 1/2 x 0.625 x (100)2 J = 3125 J
Angular momentum,
L = Iw = 0.625 x 100 Js= 62.5 Js.


Question 7. 15. To maintain a rotor at a uniform angular speed of 200 rad s-1, an engine needs to transmit a torque of 180 Nm. What is the power required by the engine?
Note: Uniform angular velocity in the absence of friction implies zero torque. In practice, applied torque is needed to counter fricitional torque). Assume that the engine is 100 efficient.
Answer: Here, a = 200 rad s-1; Torque, τ= 180 N-m
Since,Power, P = Torque (τ) x angular speed (w)
= 180 x 200 = 36000 watt = 36 KW.





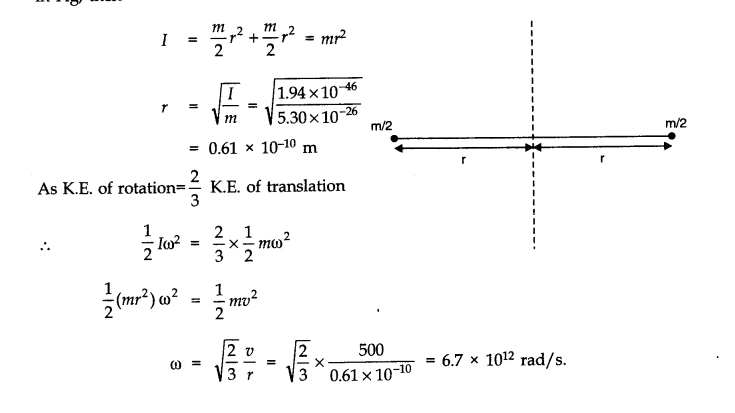
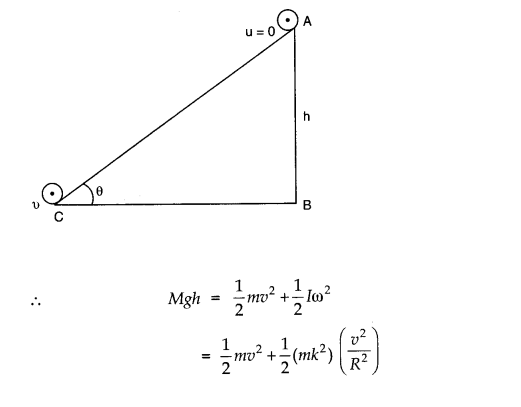
Question 7. 21. A solid cylinder rolls up an inclined plane of angle of inclination 30°. At the bottom of the inclined plane the centre of mass of the cylinder has a speed of 5 m/s.
(a) How far will the cylinder go up the plane?
(b) How long will it take to return to the bottom?
Answer: Here, θ= 30°, v = 5 m/ s
Let the cylinder go up the plane up to a height h.
From 1/2 mv2 +1/2IW2 = mgh



Question 7. 23. A man stands on a rotating platform, with his arms stretched horizontally holding a 5 kg weight in each hand. The angular speed of the platform is 30 revolutions per minutes. The man then brings his arms close to his body with the distance of each weight from the axis changing from 90 cm to 20 cm. The moment of inertia of the man together with the platform may be taken to be constant and equal to 7.6 kg m2.(a) What is his new angular speed? (Neglect friction)(b) Is kinetic energy conserved in the process? If not, from where does the change come about?
Answer: Here, I1= 7.6 + 2 x 5 (0.9)2 = 15.7 kg m2
w1 = 30 rpm
I2 = 7.6 + 2 x 5 (0.2)2 = 8.0 kg m2
w2 = ?
According to the principle of conservation of angular momentum,
I2w2=I1w1
w2= I1/I2 w1= 15.7 x 30 /8.0 = 58.88 rpm
No, kinetic energy is not conserved in the process. In fact, as moment of inertia decreases, K.E. of rotation increases. This change comes about as work is done by the man in bringing his arms closer to his body.
Question 7. 24. A bullet of mass 10 g and speed 500 m/s is fired into a door and gets embedded exactly at the centre of the door. The door is 1.0 m wide and weighs 12 kg. It is hinged at one end and rotates about a vertical axis practically without friction. Find the angular speed of the door just after the bullet embeds into it.(Hint: The moment of inertia of the door about the vertical axis at one end is ML2/3.)
Answer: Angular momentum imparted by the bullet, L = mv x r
=(10 x 10-3) x 500 x 1/2 =2.5
Also,I=ML2/3=12 x (1.0)2/3=4 kg m2
Since L=Iw
w=L/I=2.5/4=0.625 rad / s
Question 7. 25. Two discs of moments of inertia I1 and I2 about their respective axes (normal to the disc and passing through the centre), and rotating with angular speed w1 and w2 are brought into contact face to face with their axes of rotation coincident, (a) What is the angular speed of the two-disc system? (b) Show that the kinetic energy of the combined system is less than the sum of the initial kinetic energies of the two discs. How do you account for this loss in energy? Take w1 not equal to w2.
Answer: (a) Let I1 and I2 be the moments of inertia of two discs having angular speeds w1, and w2 respectively. When they are brought in contact, the moment of inertia of the two-disc system will be I1 + I2. Let the system now have an angular speed w. From the law of conservation of angular momentum, we know that


Question 7. 26. (a) Prove the theorem of perpendicular axes.
Hint: Square of the distance of a point (x, y) in the x-y plane from an axis through the origin perpendicular to the plane is x2 + y2]
(b) Prove the theorem of parallel axes.
Hint: If the centre of mass of chosen the origin [Σ miri= 0]
Answer: (a) The theorem of perpendicular axes: According to this theorem, the moment of inertia of a plane lamina (i.e., a two dimensional body of any shape/size) about any axis OZ perpendicular to the plane of the lamina is equal to sum of the moments of inertia of the lamina about any two mutually perpendicular axes OX and OY in the plane of lamina, meeting at a point where the given axis OZ passes through the lamina. Suppose at the point ‘R’ m{ particle is situated moment of inertia about Z axis of lamina
= moment of inertia of body about x-axis
= moment of inertia of body about the y-axis.



Question 7. 27. Prove the result that the velocity v of translation of a rolling body (like a ring, disc, cylinder or sphere) at the bottom of an inclined plane of a height h is given by,v2=2gh/(1+k2/R2) using dynamical consideration (i.e., by consideration of forces and torques). Note k is the radius of gyration of the body about its symmetry axis, and R is the radius of the body. The body starts from rest at the top of the plane.
Answer: Let a rolling body (I = Mk2) rolls down an inclined plane with an initial velocity u = 0; When it reaches the bottom of inclined plane, let its linear velocity be v. Then from conservation of mechanical energy, we have Loss in P.E. = Gain in translational K.E. + Gain in rotational K.E.

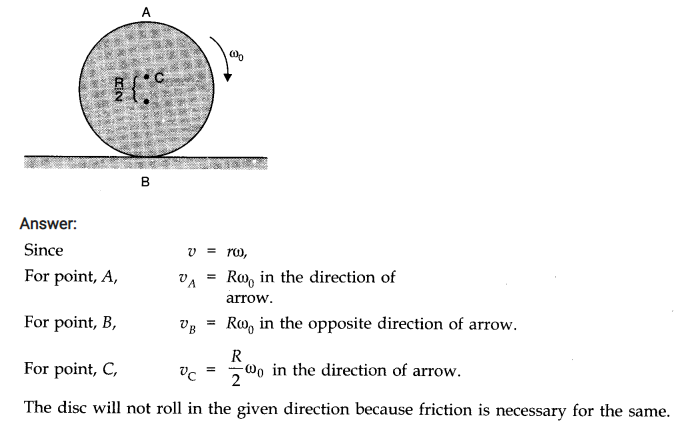
Question 7. 29. Explain why friction is necessary to make the disc roll (refer to Q. 28) in the direction indicated.
(a) Give the direction of frictional force at B, and the sense of frictional torque, before perfect rolling begins.
(b) What is the force of friction after perfect rolling begins?
Answer: To roll a disc, we require a torque, which can be provided only by a tangential force. As force of friction is the only tangential force in this case, it is necessary.
(a)As frictional force at B opposes the velocity of point B, which is to the left, the frictional force must be to the right. The sense of frictional torque will be perpendicular to the plane of the disc and outwards.
(b)As frictional force at B decreases the velocity of the point of contact B with the surface, the perfect rolling begins only when velocity of point B becomes zero. Also, force of friction would become zero at this stage.




Question 7. 32. Read each statement below carefully, and state, with reasons, if it is true or false:
(a) During rolling, the force of friction acts in the same direction as the direction of motion of the CM of the body.
(b) The instantaneous speed of the point of contact during rolling is zero.
(c) The instantaneous acceleration of the point of contact during rolloing is zero.
(d) For perfect rolling motion, work done against friction is zero.
(e) A wheel moving down a perfectly frictionless inclined plane will undergo slipping (not rolling) motion.
Answer: (a) True. When a body rolls without slipping, the force of friction acts in the same
direction as the direction of motion of the centre of mass of rolling body.
(b) True. This is because rolling body can be imagined to be rotating about an axis passing through the point of contact of the body with the ground. Hence its instantaneous speed is zero.
(c) False. This is because when the body is rotating, its instantaneous acceleration is not zero.
(d) True. For perfect rolling motion as there is no relative motion at the point of contact, hence work done against friction is zero.
(e) True. This is because rolling occurs only on account of friction which is a tangential force capable of providing torque. When the inclined plane is perfectly smooth, it will simply slip under the effect of its own weight.