Atmospheric Pressure

• Pressure exerted by the weight of the atmosphere.
• Atmosphere is a mixture of different gases. All these gas molecules together constitute some weight. By virtue of this weight there is some pressure exerted by the atmosphere on all the objects.
• This pressure is known as atmospheric pressure.
• Value of atmospheric pressure at sea level is 1.01*10⁵
• 1atm = 1.01*10⁵Pa

Problem:- What is the pressure inside the drop of mercury of radius 3.00 mm at room temperature? Surface tension of mercury at that temperature (20°C) is 4.65 × 10^–1 N m^–1. The atmospheric pressure is 1.01 × 10⁵ Pa. Also give the excess pressure inside the drop.

Answer:-

Radius of the mercury drop, r = 3.00 mm = 3 × 10^–3 m

Surface tension of mercury, S = 4.65 × 10^–1 N m^–1

Atmospheric pressure, P₀ = 1.01 × 10⁵ Pa

Total pressure inside the mercury drop

= Excess pressure inside mercury + Atmospheric pressure

=2S/r + P₀

= (2×4.65×10^-1)/(3×10^-3)

= 1.0131 × 10⁵ = 1.01 ×10⁵ Pa

Excess pressure = 2S/r = (2×4.65×10^-1)/3×10^-3

= 310 Pa

How to measure atmospheric pressure?

• Atmospheric pressure is measured by Mercury Barometer.
• Mercury barometer consists of trough filled with mercury(Hg).There is a tube which also contains mercury and it is invertedinside the trough.
• The one end of tube is closed and other end of the tube is placed inverted inside the trough.
• The inverted tube which also contains mercury up to a certain level and the space above mercury in the tubeis occupied by the vapours of mercury. The pressure can be considered as 0 at this place.
• The atmosphere will exert some atmospheric pressure on the mercury level as a result the level of mercury decreases in the trough andit increases in the tube.
• This increase in level will determine how much pressure was exerted by the atmosphere.
• The pressure exerted is directly ∝to the increase in the mercury column of the tube.
• We can say that pressure at point A is same as pressure at point B.
• P_atm=hρg.
• It is measured in terms of how many mm of Hg rose in the column.
• Greater the height greater is the atmospheric pressure.
• When the height in this column becomes 76cm Hg we can say that the pressure applied is equal to 1atm.

Units of Pressure:-

1.SI unit: Pascal (Pa)

• Pressure is always measured by taking sea level as the reference level. At sea level P=1.01*10⁵ Pa.

2. Atmosphere (atm)
   • Reference level is at sea level.
   • Pressure equivalent of 76cm of Hg column
   • 1atm=76cm of Hg column
   • 1atm=1.01*10⁵ Pa
   •  
3. Torr

• Pressure equivalent of 1mm of Hg column.
• 1torr =133 Pa

4. Bar

• 1bar = 10⁵ Pa

Problem:- A U-shaped wire is dipped in a soap solution, and removed. The thin soap film formed between the wire and the light slider supports a weight of 1.5 × 10^–2 N (which includes the small weight of the slider). The length of the slider is 30 cm. What is the surface tension of the film?

Answer

The weight that the soap film supports, W = 1.5 × 10^–2 N

Length of the slider, l = 30 cm = 0.3 m

A soap film has two free surfaces.

Total length = 2l = 2 × 0.3 = 0.6 m

Surface tension, S = (Force or Weight)/2l

=(1.5×10^-2)/0.6 = 2.5×10^-2N/m

Therefore, the surface tension of the film is 2.5 × 10^–2 N m^–1

Gauge Pressure

• Pressure difference between the system and the atmosphere.
• From relation P=P_a+ ρgh where P= pressure at any point, P_a = atmospheric pressure.
• We can say that Pressure at any point is always greater than the atmospheric pressure by the amount ρgh.
• P-P_a=ρgh where
• P =pressure of the system, P_a=atmospheric pressure,
• (P-P_a) = pressure difference between the system and atmosphere.
• hρg = Gauge pressure.

How to measure Gauge pressure

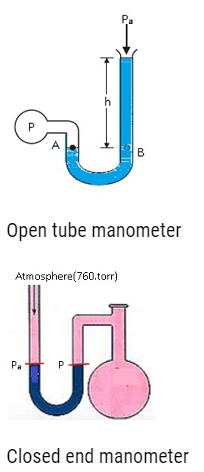
• Gauge pressure is measured by Open Tube Manometer.
• Open Tube Manometer is a U-shaped tube which is partially filled with mercury(Hg).
• One end is open and other end is connected to some device where pressure is to be determined.This means it is like a system.
• The height to which the mercury column will rise depends on the atmospheric pressure. Similarly depending on the pressure of the system the height of mercury in another tube rises.
• The pressure difference between these two heights is the difference between the atmospheric pressure and system.
• This difference in pressure is the gauge pressure.
• Consider if the level of mercury column is same in both the U-tubes.
• P_atm=P, therefore the difference between the atmospheric pressure and the pressure of the system is 0.
• Gauge Pressure is 0.
• P_atm = 760torr.

Problem:- What is the excess pressure inside a bubble of soap solution of radius 5.00 mm, given that the surface tension of soap solution at the temperature (20 °C) is 2.50 × 10^–2 N m^–1? If an air bubble of the same dimension were formed at depth of 40.0 cm inside a container containing the soap solution (of relative density 1.20), what would be the pressure inside the bubble? (1 atmospheric pressure is 1.01 × 10⁵ Pa).

Answer:

Excess pressure inside the soap bubble is 20 Pa;

Pressure inside the air bubble is

Soap bubble is of radius, r = 5.00 mm = 5 × 10^–3 m

Surface tension of the soap solution, S = 2.50 × 10^–2 Nm^–1

Relative density of the soap solution = 1.20

Density of the soap solution, ρ = 1.2 × 10³ kg/m³

Air bubble formed at a depth, h = 40 cm = 0.4 m

Radius of the air bubble, r = 5 mm = 5 × 10^–3 m

1 atmospheric pressure = 1.01 × 10⁵ Pa

Acceleration due to gravity, g = 9.8 m/s²

Hence, the excess pressure inside the soap bubble is given by the relation:

P=4S/r

=(4×2.5×10^-2)/5×10^-3

=20Pa

Therefore, the excess pressure inside the soap bubble is 20 Pa.

The excess pressure inside the air bubble is given by the relation:

P’=2S/r

=(2×2.5×10^-2)/5×10^-3

=10Pa

Therefore, the excess pressure inside the air bubble is 10 Pa.

At a depth of 0.4 m, the total pressure inside the air bubble

= Atmospheric pressure + hρg + P’

=1.01×10⁵+0.4×1.2×10³x9.8+10

=1.057×10⁵Pa

=1.06×10⁵Pa

Therefore, the pressure inside the air bubble is 1.06×10⁵Pa.

Absolute Pressure

• Absolute pressure is defined as the pressure above the zero value of pressure.
• It is the actual pressure which a substance has.
• It is measured against the vacuum.
• Absolute pressure is measured relative to absolute zero pressure.
• It is sum of atmospheric pressure and gauge pressure.
• P =P_a+hρg where P = pressure at any point, P_a = atmospheric pressure and hρg= gauge pressure.
• Therefore P =P_a + Gauge Pressure. Where P = absolute pressure.
• It is measured with the help of barometer.

Problem:  The density of theatmosphere at sea level is 1.29 kg/m³.Assume that it does not change withaltitude. Then how high would theatmosphere extend?

Answer:

From equation: – P=P_a+ρgh

ρgh = 1.29 kg m^–3 × 9.8 m s² × h m = 1.01 × 10⁵ Pa

∴ h = 7989 m ≈ 8 km

In reality the density of air decreases withheight. So does the value of g. The atmospheric

cover extends with decreasing pressure over100 km. We should also note that the sea level

atmospheric pressure is not always 760 mm ofHg. A drop in the Hg level by 10 mm or more isa sign of an approaching storm.

Problem:- At a depth of 1000 m in anocean (a) what is the absolute pressure?(b) What is the gauge pressure? (c) Findthe force acting on the window of 20 cm × 20 cm of a submarine at this

depth, the interior of which is maintainedat sea-level atmospheric pressure. (Thedensity of sea water is 1.03 × 10³ kg m^-3,g = 10m s^–2.)

Answer:

Here h = 1000 m and ρ = 1.03 × 10³ kg m^-3.

(a) From Eq. P₂ − P₁= ρgh, absolute pressure

P = P_a + ρgh

= 1.01 × 10⁵ P_a+ 1.03 × 10³ kg m^–3 × 10 m s^–2 × 1000 m

= 104.01 × 10⁵ Pa

≈ 104 atm

(b) Gauge pressure is P − P_a = ρgh = P_g

P_g = 1.03 × 10³ kg m^–3 × 10 ms² × 1000 m

= 103 × 10⁵ Pa

≈ 103 atm

(c) The pressure outside the submarine isP = P_a + ρgh and the pressure inside it isP_a. Hence, the net pressure acting on thewindow is gauge pressure, P_g = ρgh. Sincethe area of the window is A = 0.04 m², theforce acting on it is

F = P_g A = (10³ × 10⁵ Pa) × 0.04 m² = 4.12 × 10⁵ N