Venturimeter

• Venturimeter is a device to measure the flow of incompressible liquid.
  • It consists of a tube with a broad diameter having a larger cross-sectional area but there is a small constriction in the middle.
  • It is attached to U-tube manometer. One end of the manometer is connected to the constriction and the other end is connected to the broader end of the Venturimeter.
  • The U-tube is filled with fluid whose density is ρ.
  • A₁= cross-sectional area at the broader end, v₁ = velocity of the fluid.
  • A₂=cross-sectional area at constriction, v₂= velocity of the fluid.
• By the equation of continuity, wherever the area is more velocity is less and vice-versa.As A₁ is more this implies v₁ is less and vice-versa.
• Pressure is inversely ∝ to Therefore at A₁ pressureP₁ is less as compared to pressure P₂ at A₂.
  • This implies P₁<P₂ as v₁>v₂.
• As there is difference in the pressure the fluid moves,this movement of the fluid is marked by the level of the fluid increase at one end of the U-tube.

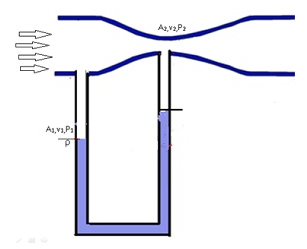
A schematic diagram of Venturimeter

Venturimeter: determining the fluid speed

• By Equation of Continuity: -A₁v₁=A₂v₂.
• This implies v₂=(A₁/A₂)v₁ (Equation(1))
• By Bernoulli’s equation:- P₁ + (1/2) ρ v₁² + ρg h = (1/2) ρ v₂² + ρg h
  • As height is same we can ignore the term ρg
  • This implies P₁-P₂=(1/2) ρ(v₂²– v₁²)
  • =1/2ρ(A₁²/A₂²v₁²– v₁²)(Using equation(1)
  • =1/2ρv₁²(A₁²/A₂² -1)
  • =1/2ρv₁²(A₁²/A₂²-1)
• As there is pressure difference the level of the fluid in the U-tube changes.
• (P₁-P₂) = hρ_mgwhere ρ_m(density of the fluid inside the manometer).
• 1/2ρv₁²(A₁²/A₂²-1)=hρ_mg
• v₁ = 2hρ_mg/ρ[A₁²/A₂²-1]^-1/2

Practical Application of Venturimeter:

1. Spray Gun or perfume bottle- They are based on the principle of Venturimeter.

• Consider a bottle filled with fluidand having a pipe which goes straight till constriction.There is a narrow end of pipewhich has a greater cross sectional area.
• The cross sectional area of constriction which is at middle is less.
• There is pressure difference when we spray as a result some air goes in ,velocity of the air changes depending on the cross sectional area.
• Also because of difference in cross sectional area there is pressure difference, the level of the fluid rises and it comes out.

Problem:- The flow of blood in a large artery of an anesthetiseddog is diverted through a Venturimeter.The wider part of the meter has a crosssectionalarea equal to that of the artery.A = 8 mm². The narrower part has an areaa = 4 mm². The pressure drop in the artery is 24 Pa. What is the speed of the blood inthe artery?

Answer: –The density of blood is 10.1 to be 1.0⁶ × 10³ kg m^-3. The ratio of the

areas is(A/a) = 2.

Using Equation = 2hρ_mg/ρ[A₁²/A₂²-1]^-1/2

v₁=√2x24Pa/(1060kgm^-3x (2²-1)) = 0.125ms^-1.

Dynamic Lift

• Dynamic lift is the normal force that acts on a body by virtue of its motion through a fluid.
• Consider an object which is moving through the fluid,and due to the motion of the object through the fluid there is a normal force which acts on the body.
• This force is known as dynamic lift.
• Dynamic lift is most popularly observed in aeroplanes.
  • Whenever an aeroplane is flying in the air, due to its motion through the fluid here fluid is air in the atmosphere.Due to its motion through this fluid, there is a normal force which acts on the body in the vertically upward direction.
  • This force is known as Dynamic lift.
• Examples:
  • Airplane wings
  • Spinning ball in air

Magnus Effect

• Dynamic lift by virtue of spinning is known as Magnus effect.
• Magnus effect is a special name given to dynamic lift by virtue of spinning.
• Example:-Spinning of a ball.
  • Case1:-When the ball is not spinning.
    • The ball moves in the air it does not spin, the velocity of the ball above and below the ball is same.
    • As a result there is no pressure difference.(ΔP= 0).
    • Therefore there is no dynamic lift.

Problem:- In a test experiment on a model aeroplane in a wind tunnel, the flow speeds on the upper and lower surfaces of the wing are 70 m s^–1 and 63 m s^–1 respectively. What is the lift on, the wing if its area is 2.5 m²? Take the density of air to be 1.3 kg m^–3.

Answer:

Speed of wind on the upper surface of the wing, V₁ = 70 m/s

Speed of wind on the lower surface of the wing, V₂ = 63 m/s

Area of the wing, A = 2.5 m²

Density of air, ρ = 1.3 kg m^–3

According to Bernoulli’s theorem, we have the relation:

Where,

P₁+1/2 (ρ V₁²) = P₂+1/2(ρV₂²)

P₂-P₁ = 1/2 ρ (V₁² – V₂²)

P₁ = Pressure on the upper surface of the wing

P₂ = Pressure on the lower surface of the wing

The pressure difference between the upper and lower surfaces of the wing provides lift

to the aeroplane.

Dynamic Lift on the wing = (P₂-P₁) A

=1/2 ρ (V₁² – V₂²) A

=1.3((70)² – (63)²) x2.5

= 1512.87

= 1.51 × 10³ N

Therefore, the lift on the wing of the aeroplane is 1.51 × 10³ N.

Problem:- A fully loaded Boeing aircraft has a mass of 3.3×10⁵kg.Its total wing area is 500m².It is a level flight with a speed of 960km/h.Estimate the pressure difference between the lower and upper surfaces of the wings.

Answer:-

Weight of the aircraft= Dynamic lift

mg = (P₁-P₂) A

mg/A=ΔP

ΔP=3.3×10⁵x9.8/500

=6.5×10³N/m²