Beats

Beats is the phenomenon caused by two sound waves of nearly same frequencies and amplitudes travelling in the same direction.

For example:-

• Tuning of musical instruments like piano, harmonium etc. Before we start playing on these musical instruments they are set against the standard frequency. If it is not set a striking noise will keep on coming till it is set.

Mathematically

• Consider only the time dependent and not the position dependent part of the wave.
• s₁=a cos ω₁t and s₂=a cos ω₂t; where amplitude and phase of the waves are same,but the frequencies are varying. Also considering ω₁> ω₂.
• When these 2 waves superimpose s= s₁+ s₂=a[cos ω₁t + cos ω₂t]
• By simplifying , 2a (cos(ω₁ – ω₂)/2)t cos(ω₁ + ω₂)/2)t)
• =>ω₁ – ω₂ is very small as ω₁> ω₂.Let (ω₁ – ω₂ )=ω_b
• =>ω₁ + ω₂ is very large. Let (ω₁ + ω₂ )=ω_a
• s= 2a cos ω_bt cos ω_at
• cosω_at will vary rapidly with time and 2acosω_bt will change slowly with time.
• Therefore we can say 2acosω_bt = constant. As a result 2acosω_bt = amplitude as it has small angular variation.

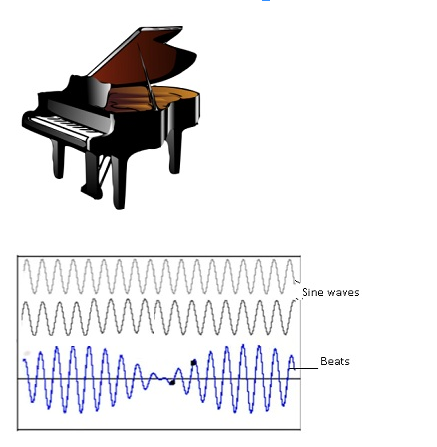
Problem:- Two sitar strings A and Bplaying the note ‘Dha’ are slightly out oftune and produce beats of frequency 5 Hz.The tension of the string B is slightlyincreased and the beat frequency is foundto decrease to 3 Hz. What is the originalfrequency of B if the frequency of A is 427 Hz?

Answer:-  Increase in the tension of a stringincreases its frequency. If the original frequencyof B (ν_B) were greater than that of A (ν_A), furtherincrease in ν_B should have resulted in anincrease in the beat frequency. But the beatfrequency is found to decrease. This shows thatν_B< ν_A. Since ν_A – ν_B = 5 Hz, and ν_A = 427 Hz, weget ν_B = 422 Hz.

Doppler’s Effect

• Doppler Effect is the phenomenon of motion-related frequency change.
• Consider if a truck is coming from very far off location as it approaches near our house, the sound increases and when it passes our house the sound will be maximum. And when it goes away from our house sound decreases.
• This effect is known as Doppler Effect.
• A person who is observing is known as Observer and object from where the sound wave is getting generated it is known as Source.
• When the observer and source come nearer to each other as a result waves get compressed. Therefore wavelength decreases and frequency increases.
• Case 1:- stationary observer and moving source
• Let the source is located at a distance L from the observer.
• At any time t₁, the source is at position P₁.
• Time taken by the wave to reach observer =L/v where v=speed of the sound wave.
• After some time source moves to position P₀ in time T₀.
• Distance between P₁ and P₀ =v_sT_o where v_s is the velocity of the source.
• Let t₂be the time taken by the second wave to reach the observer
  • Total time taken by the for the second wave to be sent to the observer = T_o +( L+v_sT_o)/v
  • Total time taken by the for the third wave to be sent to the observer=2T_o +( L+2v_sT_o)/v
  • Therefore for nth point t_n+1 =nT_o +( L+nv_sT_o)/v
  • =>In time t_n+1the observer captures n waves.
• Total time taken by the waves to travel Time period T= (t_n+1 – t₁)/n
• =T_o +(v_sT_o)/v =>T=T_o(1+v_s/v)
• Or v= 1/T
• =>v = v₀(1+v_s/v)^-1
• By using binomial Theorem,v= v₀ (1- v_s/v)
• If the source is moving towards the observer the expression will become v= v₀ (1+ v_s/v)
• Case 2:- moving observer and stationary source
• As the source is not moving therefore v_s is replaced by -v₀.
• Therefore v= v₀ (1+ v₀/v)