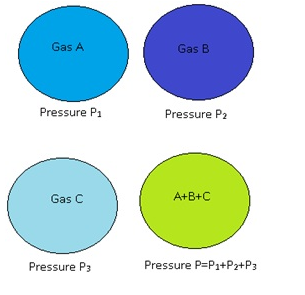
Deducing Dalton’s Law of partial pressures

• Dalton’s law of partial pressure states that the total pressure of a mixture of ideal gases is the sum of partial pressures.
• Consider if there are several ideal gases mixed together in a vessel,then the total pressure of that vessel is equal to sum of partial pressure.
• Partial pressure is the pressure exerted by a particular gas if only that gas is present in the vessel.
• For example: –
  • Consider if in a vessel there is a mixture of 3 gases, A,B and C.So the partial pressure of A is equal to pressure exerted only by Aand considering B and C are not present.
  • Similarly partial pressure of B is equal to the pressure exerted only by B and considering A and C are not there.
  • Similarly for C.

• According to Dalton’s law the total pressure of mixture is sum of partial pressure of A, partial pressure of B and partial pressure of C.

To show how perfect gas equation concludes Dalton’s law of partial pressure:-

• Suppose there is a mixture of ideal gases which means these gases do not interact with each other.
  • By perfect gas equation PV=μRT
    • Where V=volume of vessel,P=Pressure and T=temperature andμ (no. of moles).
  • As there are mixture of gases therefore μ=μ₁+μ₂+ —- so on.
  • PV=( μ₁+μ₂)RT
  • P=( μ₁+μ₂)RT/V =>μ₁RT/V + μ₂RT/V + —
    • P=P₁+P₂ +—-
      • Where P₁=partial pressure of gas 1 and P₂=partial pressure of gas 2.
    • Therefore P= P₁+P₂+—total pressure due to the mixture of gases is equal to the sum of the partial pressure of the gas.

Problem: -Estimate the fraction of molecular volume to the actual volume occupied by oxygen gas at STP. Take the diameter of the oxygen to be 3Å.

Answer:- At STP, Temperature = 273K and Pressure=1atm, diameter=3Å =3×10^-8 cm.

Actual volume by 1mole O₂ gas at STP =22.4l = 22400cm³.

Molecular volume of O₂ = (4/3) πr³xN_A

= (4/3) 3.14x (1.5×10^-8)³x6.02×10²³ =8.51cm³

Therefore, Ratio =8.51/22400 = 3.8×10^-4

Problem:- The density of water is 1000kg m^–3. The density of water vapour at 100 °Cand 1 atm pressure is 0.6 kg m^–3. Thevolume of a molecule multiplied by the totalnumber gives, what is called, molecularvolume. Estimate the ratio (or fraction) ofthe molecular volume to the total volumeoccupied by the water vapour under theabove conditions of temperature andpressure.

Answer:- For a given mass of water molecules,the density is less if volume is large. So the volume of the vapour is 1000/0.6 = /(6 ×10 ^-4 )times larger. If densities of bulk water and watermolecules are same, then the fraction ofmolecular volume to the total volume in liquidstate is 1. As volume in vapour state hasincreased, the fractional volume is less by thesame amount, i.e. 6×10^-4.

Problem: –  Estimate the volume of awater molecule if the density of water is 1000kg m^–3. The density of water vapour at 100 °Cand 1 atm pressure is 0.6 kg m^–3?

Answer: – In the liquid (or solid) phase, themolecules of water are quite closely packed. Thedensity of water molecule may therefore, beregarded as roughly equal to the density of bulkwater = 1000 kg m^–3. To estimate the volume ofa water molecule, we need to know the mass ofa single water molecule. We know that 1 moleof water has a mass approximately equal to(2 + 16)g = 18 g = 0.018 kg.

Since 1 mole contains about 6 × 10²³molecules (Avogadro’s number), the mass ofa molecule of water is (0.018)/(6 × 10²³) kg =3 × 10^–26 kg. Therefore, a rough estimate of thevolume of a water molecule is as follows:

Volume of a water molecule

= (3 × 10^–26 kg)/ (1000 kg m^–3)

= 3 × 10^–29 m³

= (4/3) π (Radius)³

Hence, Radius ≈ 2 ×10^-10 m = 2 Å.

Problem:- What is the averagedistance between atoms (interatomicdistance) in water?

Answer: A given mass of water in vapour statehas 1.67×10³ times the volume of the same massof water in liquid state. This is alsothe increase in the amount of volume availablefor each molecule of water. When volumeincreases by 10³ times the radius increases byV1/3 or 10 times, i.e., 10 × 2 Å = 20 Å. So theaverage distance is

= 2 × 20 = 40 Å.

Problem:-  A vessel contains two nonreactivegases: neon (monatomic) andoxygen (diatomic). The ratio of their partialpressures is 3:2. Estimate the ratio of (i)number of molecules and (ii) mass densityof neon and oxygen in the vessel. Atomicmass of Ne = 20.2 u, molecular mass of O₂= 32.0 u.

Answer: – Partial pressure of a gas in a mixture isthe pressure it would have for the same volumeand temperature if it alone occupied the vessel.

(The total pressure of a mixture of non-reactivegases is the sum of partial pressures due to itsconstituent gases.) Each gas (assumed ideal)obeys the gas law.

Since V and T are common tothe two gases, we have

P₁V = μ₁ RT and P₂V =μ₂RT, i.e. (P₁/P₂) = (μ₁ / μ₂).

Here 1 and 2 referto neon and oxygen respectively. Since (P₁/P₂) =(3/2) (given), (μ₁/ μ₂) = 3/2

(i) By definition μ₁ = (N₁/N_A ) and μ₂ = (N₂/N_A)where N₁ and N₂ are the number of moleculesof 1 and 2, and NA is the Avogadro’s number.

Therefore, (N₁/N₂) = (μ₁ / μ₂) = (3/2).

(ii) We can also write μ₁ = (m₁/M₁) and μ₂ =(m₂/M₂) where m₁ and m₂ are the masses of 1 and 2; and M₁ and M₂ are their molecularmasses. (Both m₁ and M₁; as well as m₂ and M₂ should be expressed in the same units).If ρ₁ and ρ₂ are the mass densities of 1 and 2 respectively, we have,

= (½) (m₁/V)/m₂/V = (m₁/m₂) (1/2) (M₁/M₂)

= (3/2) (20.2/32.0)

=0.947

Problem:- An air bubble of volume 1.0cm³ rises from the bottom of a lake 40m deep at a temperature of 12⁰C. To what volume does it grow when it reaches the surface, which is at temperatures of 35⁰C?

Answer:- Let the depth (d) of the lake = 40m. Temperature (T₁) at the bottom = 12⁰C = 285K and (V₁) Volume of air bubble= 1.0cm³ =1×10^-6m³.Temperature at the surface (T₂) =35⁰C = 308K, Pressure at the surface (P₂) = 1 atm= 1.013×10⁵ Pa.

Pressure at the bottom P₁ = P₂+ρdg 

=1+10³x9.8×40

=493300 Pa

Also (P₁V₁)/T₁= (P₂V₂)/T₂

V₂ = (P₁V₁T₂)/P₂T₁

After calculating,

V₂=5.263 cm³

Kinetic Theory of an Ideal Gas

Basis of Kinetic Theory: –

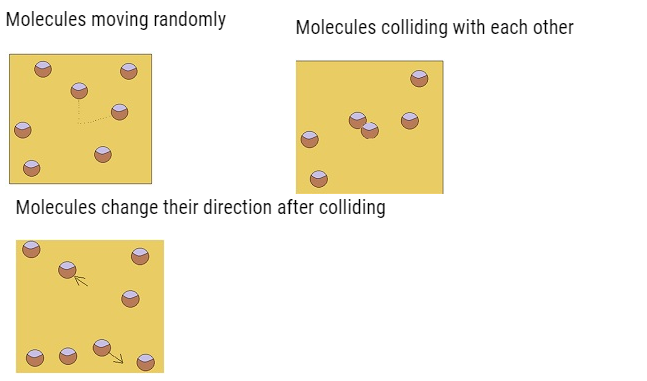
1. Molecules of gas are in incessant random motion,colliding against one another

andwith the walls of the container.

2. All collisions are elastic.
3. Total Kinetic energy is conserved.
4. Total momentumis conserved.

• In case of an elastic collision total Kinetic energy and momentum before collision is equal to the total Kinetic energy and momentum after collision.

What does Kinetic Theory tells?

1. At ordinary temperature and pressure the molecular size is very small as compared to inter molecular distance between them.
2. In case of gas, molecules are very far from each other and the size of molecules is small as compared to the distance between them.
3. As a result, interaction between them is negligible. As there is no interaction between the molecules, there will be no force between the molecules.
4. As a result molecules are moving freely as per newton’s first law of motion.
5. The molecules should move along straight line but when they come closer they experience the intermolecular forces and as a result their velocities change.
6. This phenomenon is known as collision.These collisions are elastic.

Justifying the assumptions:-

1. We have assumed the container containing the gas is a cube. The shape of the container is immaterial.
2. For a vessel of any arbitrary shape, we can choose a small infinitesimal (planar) area and can prove the above derivation.
3. We will see A and Δt are not there in the final result.
4. By Pascal’s law pressure in one portion of gas in equilibrium is the same as anywhere else.
5. All collisions are neglected.
   1. The number of molecules hitting the wall in time Δt was found to be ½ n AvxΔt, with random collisionsand asteady state of gas.
   2. Thus, if a molecule with velocity (v_x, v_y,v_z)acquires a different velocity due to collision withsome molecules, there will always be some othermolecule with a different initial velocity whichafter a collision acquires the velocity (v_x, v_y, v_z).
   3. Molecular collision, when they are not too frequent and the time spent in collision is very small compared to the time between collisions, will not have any affect in the above calculation.

Problem:-

Estimate the average thermal energy of a helium atom at (i) room temperature (27 °C),

(ii) The temperature on the surface of the Sun (6000 K), (iii) the temperature of 10 millionKelvin (the typical core temperature in the case of a star).

Answer:-

At room temperature, T = 27°C = 300 K

Average thermal energy= (3/2) kT

Where k is Boltzmann constant = 1.38 × 10^–23 m² kg s^–2 K^–1

(3/2) kT= (3/2) x1.38×10^-38x300= 6.21 × 10^–21J

Hence, the average thermal energy of a helium atom at room temperature (27°C) is

=6.21× 10^–21 J.

On the surface of the sun, T = 6000 K

Average thermal energy= (3/2) kT

= (3/2) x1.38×10^-38x6000

= 1.241 × 10^–19 J

Hence, the average thermal energy of a helium atom on the surface of the sun is

=1.241 ×10^–19 J.

At temperature, T = 10⁷ K

Average thermal energy= (3/2) kT

= (3/2) x1.38×10^-23x10⁷

= 2.07 × 10^–16 J

Hence, the average thermal energy of a helium atom at the core of a star is 2.07 ×10^–16

(ii) Now ½ m vrms2 = average kinetic energy permolecule = (3/2) k_BT where m is the massof a molecule of the gas. Therefore,

v²_rmsAr/ = v²_rmscl =M_cl/M_AR =70.9/39.9 =1.77

where M = the molecular mass of the gas.(For argon, a molecule is just an atom of argon.)

Taking square root of both sides, v_rmsAr = v_rmscl = 1.33

Problem:- Uranium has two isotopesof masses 235 and 238 units. If both arepresent in Uranium hexafluoride gas whichwould have the larger average speed? Ifatomic mass of fluorine is 19 units,estimate the percentage difference inspeeds at any temperature.

Answer:-  At a fixed temperature the averageenergy = ½ m <v2> is constant. So smaller the mass of the molecule, faster will be the speed.The ratio of speeds is inversely proportional tothe square root of the ratio of the masses. Themasses are 349 and 352 units. Sov₃₄₉ / v₃₅₂ = (352/ 349)^1/2 = 1.0044.

Hence difference= 0.44 %.[²³⁵U is the isotope needed for nuclear fission.

To separate it from the more abundant isotope²³⁸U, the mixture is surrounded by a porouscylinder.

Law of Equipartition of energy:Degrees of Freedom

• Degrees of Freedom can be defined as independent displacements or rotations that specify the orientation of a body or system.
• A molecule free to move in space needs three coordinates to specify its location.
• If it is constrained to move in a plane it needs to.
• If constrained to move along a line, it needs just one coordinate to locate it.
  • For example:-Consider a room and if we tie a thick rope from one wall to another.
  • Take a ball which is moving straight on the rope.
  • The ball has only 1 degree of freedom. It can move only in one particular dimension.
    • Consider if the ball is on the floor which is two-dimensional, then the ball can move along 2 directions.
    • The ball has 2 degree of freedoms.
      • Consider if we throw the ball in space which is 3 dimensional. Then the ball can move in 3 dimensions.
    • Therefore degree of freedom tells us in how many ways a body can move or rotate or vibrate.