

As the particle is moving in the same way the projections are also moving.
- When the particle is moving in the upper part of circle then the projections start moving towards left.
- When the particle is moving in the lower part of the circle then the projections are moving towards right.
- We can conclude that the particle is swinging from left to right and again from right to left.
- This to and fro motion is SHM.

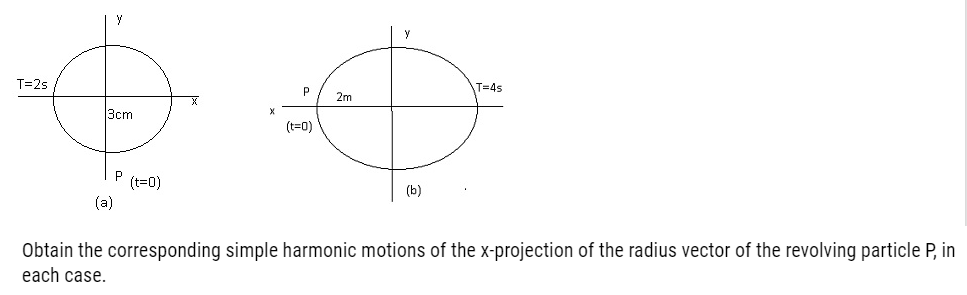
Answer: – (a) Time period, t = 2 s
Amplitude, A = 3 cm
At time, t = 0, the radius vector OP makes an angle π/2 with the positive x-axis, phase angle Φ = +π/2
Therefore, the equation of simple harmonic motion for the x-projection of OP, at the time t, is given by the displacement equation:
A= cos [(2 πt/T) + Φ]
=3cos (2 πt/2 + π/2) = -3sin (2πt/2)
=-3sinπt cm.
(b) Time Period, t = 4 s
Amplitude, a = 2 m
At time t = 0, OP makes an angle π with the x-axis, in the anticlockwise direction, Hence, phase angle Φ = +π
Therefore, the equation of simple harmonic motion for the x-projection of OP, at the time t, is given as:
=a cos [(2 πt/T) + Φ]
=2 cos [(2 πt/T) + π]
x=-2 cos (π/2 t) m
Velocity in Simple Harmonic Motion
- Uniform Circular motion can be defined as motion of an object in a circle at a constant speed.
- Consider a particle moving in circular path
- The velocity at any point P at any time t will be tangential to the point P.
- Consider θ = ωt+ φ where
- θ = angular position
- ω = angular velocity of the particle




ap = -ω2Awhere
- A = radius of the circle
- (-ive sign shows it is pointing towards the centre of the circle.)
- Consider the acceleration of the projection of the particle P’ on the x-axis.
- Accelerationwill be given as
- a(t) = -ap cosθ
- a(t) = – ap cos(ωt + φ)
- =ω2A cos (ωt + φ)
- a(t) = – ω2x(t) (Using x(t)= A cos (ωt + φ))
To verify expression for acceleration when calculated directly from SHM –
- Displacement in SHM is = A cos (ωt + φ)
- Velocity v(t) in SHM is = -Aw sin (ωt + φ)
Therefore,
- a(t) = dv/dt
- = – ω2A cos (ωt + φ)
- a(t) = – ω2x(t) (Using x(t)= A cos (ωt + φ))
Equation of acceleration of the particle which executesSHM:-
a(t) = – ω2x(t)
We can conclude that:-
- a is proportional to displacement
- acceleration is always directed towards the centre(in circular motion centre is mean position of the SHM)
From above we can say that
- SHM is the projection of the uniform circular motion such that centre of uniform circular motion becomes the mean position of the SHM and the radius of the circular motion is the amplitude of the SHM.

Problem: -A body oscillates with SHM according to the equation (in SI units), x = 5 cos [2π t + π/4]
At t = 1.5 s, calculate the (a) displacement,(b) speed and (c) acceleration of the body?
Answer:
The angular frequency ω of the body
= 2π s–1
and its time period T = 1 s.
At t = 1.5 s
(a) Displacement = (5.0 m) cos [(2π s–1)1.5 s + π/4]
= (5.0 m) cos [(3π + π/4)]
= –5.0 x 0.707 m
= –3.535 m
(b) The speed of the body
= – (5.0 m)(2π s–1) sin [(2π s–1) 1.5 s+ π/4]
= – (5.0 m) (2π s–1) sin [(3π + π/4)]
= 10π (0.707) m s–1
= 22 m s–1
(c) The acceleration of thebody
= – (2π s–1)2displacement
= – (2π s-1)2 (–3.535 m)
= 140 m s–2

F1 = -kx (force exerted by the spring onthe left side, trying to
pull the mass towards the mean position)
F2 = -kx (force exerted by the spring onthe right side, trying to pull the mass towards the mean position)
The net force, F, acting on the mass is thengiven by,
F = –2kx
Therefore, the force acting on the mass is proportional to the displacement and is directedtowards the mean position; therefore, the motion executed by the mass is simple harmonic. The time period of oscillations is given as:-
T=2π√m/2k
Problem:-The acceleration due to gravity on the surface of moon is 1.7 ms–2. What is the time period of a simple pendulum on the surface of moon if its time period on the surface of earth is 3.5 s? (g on the surface of earth is 9.8 ms–2)
Answer: -Acceleration due to gravity on the surface of moon,g’ = 1.7 m s–2
Acceleration due to gravity on the surface of earth, g = 9.8 m s–2
Time period of a simple pendulum on earth, T = 3.5 s
T=2π√l/g
where l =length of the pendulum
l= T2/ (2π) 2x g
= (3.5)2/ (4x (3.14)2) x 9.8 m
The length of the pendulum remains constant,
On moon’s surface, time period, T’= 2π√l/g’
=2π ((3.5)2/4x(3.14)2 x 9.8)/1.7
=8.4s
Hence, the time period of the simple pendulum on the surface of moon is 8.4 s.
Problem:-
(a) Time period of a particle in SHM depends on the force constant k and mass m of the particle:
T = 2π√ (m/k). A simple pendulum executes SHM approximately. Why then is the time period of a pendulum independent of the mass of the pendulum?
(b) The motion of a simple pendulum is approximately simple harmonic for small angle oscillations. For larger angles of oscillation, a more involved analysis shows that T is greater than 2π√ (l/g)
Think of a qualitative argument to appreciate this result.
(c) A man with a wristwatch on his hand falls from the top of a tower. Does the watch give correct time during the free fall?
(d) What is the frequency of oscillation of a simple pendulum mounted in a cabinthat is freely falling under gravity?
Answer:
(a) For a simple pendulum, force constant or spring factor k is proportional to mass m; therefore, m cancels out in denominator as well as in numerator. That is why the time period of simple pendulum is independent of the mass of the bob.
(b) In the case of a simple pendulum, the restoring force acting on the bob of the pendulum is given as:
F = –mg sinθ
where,
F = Restoring force
m = Mass of the bob
g = Acceleration due to gravity
θ = Angle of displacement
For small θ, sinθ≈θ
For large θ, sinθ is greater than θ.
This decreases the effective value of g.
Hence, the time period increases as:
T = 2π√ (l/g)
(c) Yes, because the working of the wrist watch depends on spring action and it has nothing to do with gravity.
(d) Gravity disappears for a man under free fall, so frequency is zero