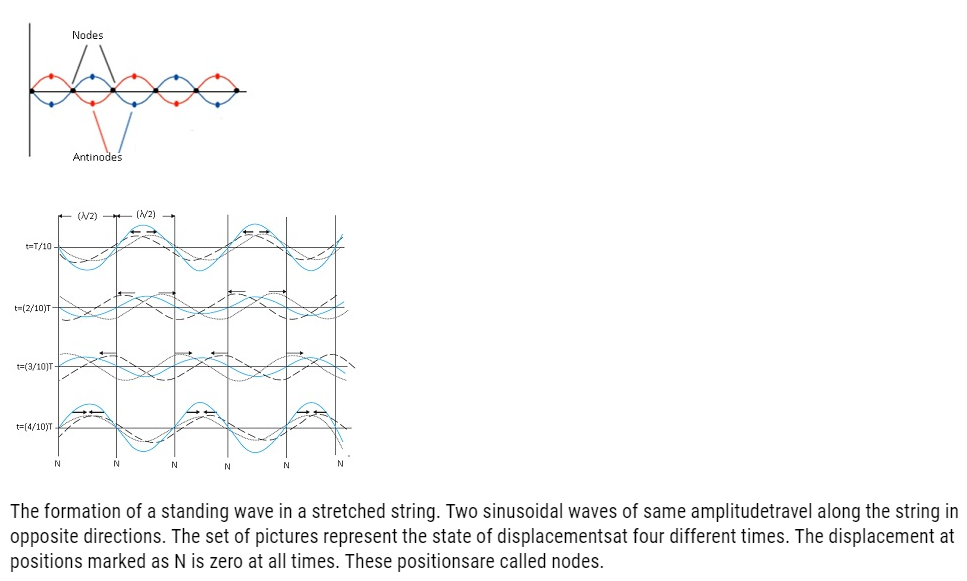
Nodes and Antinodes of Standing Wave

• The amplitude of a standing wave doesn’t remain the same throughout the wave.
• It keeps on changing as it is a function of x.
• At certain positions the value of amplitude is maximum and at certain positions the value of amplitude is 0.
• Nodes: – Nodes represent the positions of zero amplitude.
• Antinodes: – Antinodes represent the positions of maximum amplitude.

Nodes:-

• At nodes, amplitude is 0.
• In case of the standing wave amplitude is given as :- 2asinkx
• => 2asinkx = 0 ,=>sinkx = 0,=>sinkx =sin n π => kx=n π
• The value of x represents position of nodes where amplitude is 0.
• x=(nπ)/k … equation(i)
• From the definition of k=(2π)/λ … equation(ii)
• The position of nodes is represented by: –x=(n λ)/2from(i) and (ii),where n=1, 2, 3…
• Note: –Half a wavelength (λ/2) separates two consecutive nodes.

Nodes and Antinodes: system closed at both ends

• System closed at both ends means both the ends are rigid boundaries.
• Whenever there is rigid body there is no displacement at the boundary. This implies at boundary amplitude is always 0. Nodes are formed at boundary.
• Standing waves on a string of length L fixed at both ends have restricted wavelength.
• This means wave will vibrate for certain specific values of wavelength.
• At both ends,nodes will be formed.=>Amplitude=0.
• Expression for node x =(nλ)/2.This value is true when x is 0 and L.
• When x=L:- L=(nλ)/2 =>λ=(2L)/n ; n=1,2,3,4,…..
• λ cannot take any value but it can take values which satisfy λ=(2L)/n this expression.
• That is why we can say that the standing wave on a string which is tied on both ends has the restricted wavelength.
• As wavelength is restricted therefore wavenumber is also restricted.
• ν =v/λ (relation between wavelength and frequency)
• Corresponding frequencies which a standing wave can have is given as: –ν= (vn)/2Lwhere v= speed of the travelling wave.
• These frequencies are known as natural frequency or modes of oscillations.