QUESTIONS FROM TEXTBOOK ( Mechanical Properties of Fluids )
Question 10. 1. Explain why
(a) The blood pressure in humans is greater at the feet than at the brain.
(b) Atmospheric pressure at a height of about 6 km decreases to nearly half of its value at the sea level, though the height of the atmosphere is more than 100 km.
(c) Hydrostatic pressure is a scalar quantity even though pressure is force divided by area.
Answer: (a) The height of the blood column is more for the feet as compared to that for the brain.
Consequently, the blood pressure in humans is greater at the feet than at the brain.
(b) The variation of air-density with height is not linear. So, pressure also does not reduce linearly with height. The air pressure at a height h is given by P = P0e–αh where P0 represents the pressure of air at sea-level and α is a constant.
(c) Due to applied force on liquid, the pressure is transmitted equally in all directions inside the liquid. That is why there is no fixed direction for the pressure due to liquid. Hence hydrostatic pressure is a scalar quantity.
Question 10. 2. Explain why
(a) The angle of contact of mercury with glass is obtuse, while that of water with glass is acute.
(b) Water on a clean glass surface tends to spread out while mercury on the same surface tends to form drops. (Put differently, water wets glass while mercury does not.)
(c) Surface tension of a liquid is independent of the area of the surface.
(d) Water with detergent dissolved in it should have small angles of contact.
(e) A drop of liquid under no external forces is always spherical in shape.
Answer: (a) Let a drop of a liquid L be poured on a solid surface S placed in air A. If TSL,and TSA be the surface tensions corresponding to solid-liquid layer, liquid-air layer and solid-air layer respectively and θ be the angle of contact between the liquid and solid, then

(c) Surface tension of liquid is the force acting per unit length on a line drawn tangentially to the liquid surface at rest. Since h as force is independent of the area of liquid surface therefore, surface tension is also independent of the area of the liquid surface.
(d) We know that the clothes have narrow pores or spaces which act as capillaries. Also, we know that the rise of liquid in a capillary tube is directly proportional to cosθ (Here θ is the angle of contact). As θ is small for detergent, therefore cos θ will be large. Due to this, the detergent will penetrate more in the narrow pores of the clothes.
(e) We know that any system tends to remain in a state of minimum energy. In the absence of any external force for a given volume of liquid its surface area and consequently. Surface energy is least for a spherical shape. It is due to this reason that a liquid drop, in the absence of an external force is spherical in shape.
Question 10. 3. Fill in the blanks using the words from the list appended with each statement:
(a) Surface tension of liquids generally…………….with temperature. (increases/decreases)
(b) Viscosity of gases………………..with temperature, whereas viscosity of liquids…………..with temperature. (increases/decreases)
(c) For solids with elastic modulus of rigidity, the shearing force is proportional to…………………..while for fluids it is proportional to…………. (shear strain/rate of shear strain)
(d) For a fluid in steady flow, the increases inflow speed at a constriction follows from…………………………. while the decrease of pressure there follows from………………….(conservation of mass/Bernoulli’s principle)
(e) For the model of a plane in a wind tunnel, turbulence occurs at a…………….speed than the critical speed for turbulence for an actual plane. (greater/smaller)
Answer: (a), decreases
(b) increases; decreases
(c) shear strain; rate of shear strain
(d) conservation of mass; Bernoulli’s principle
(e) greater
Question 10. 4. Explain why
(a) To keep a piece of paper horizontal, you should blow over, not under, it.
(b) When we try to close a water tap with our fingers, fast jets of water gush through the openings between our fingers.
(c) The size of a needle of a syringe controls flow rate better than the thumb pressure exerted by a doctor while administering an injection.
(d) A fluid flowing out of a small hole in a vessel results in a backward thurst on the vessel.
(e) A spinning cricket ball in air does not follow a parabolic trajectory.
Answer: (a) When we blow over the piece of paper, the velocity of air increases. As a result, the pressure on it decreases in accordance with the Bernoulli’s theorem whereas the pressure below remains the same (atmospheric pressure). Thus, the paper remains horizontal.
(b) By doing so the area of outlet of water jet is reduced, so velocity of water increases according to equation of continuity av = constant.
(c) For a constant height, Bernoulli’s theorem is expressed as P +1/2 ρ v2 = Constant
In this equation, the pressure P occurs with a single power whereas the velocity occurs with a square power. Therefore, the velocity has more effect compared to the pressure. It is for this reason that needle of the syringe controls flow rate better than the thumb pressure exerted by the doctor.
(d) This is because of principle of conservation of momentum. While the flowing fluid carries forward momentum, the vessel gets a backward momentum.
(e) A spinning cricket ball would have followed a parabolic trajectory has there been no air. But because of air the Magnus effect takes place. Due to the Magnus effect the spinning cricket ball deviates from its parabolic trajectory.


Question 10. 7. A vertical off-shore structure is built to withstand a maximum stress of 109 Pa. Is the structure suitable for putting up on top of an oil well in the ocean? Take the depth of the ocean to be roughly 3 km, and ignore ocean currents.
Answer: Here, Maximum stress = 109 Pa, h = 3 km = 3 x 103 m;
p (water) = 103 kg/m3 and g = 9.8 m/s2.
The structure will be suitable for putting upon top of an oil well provided the pressure exerted by sea water is less than the maximum stress it can bear.
Pressure due to sea water, P = hρg = 3 x 103 x 103x 9.8 Pa = 2.94 x 107 Pa
Since the pressure of sea water is less than the maximum

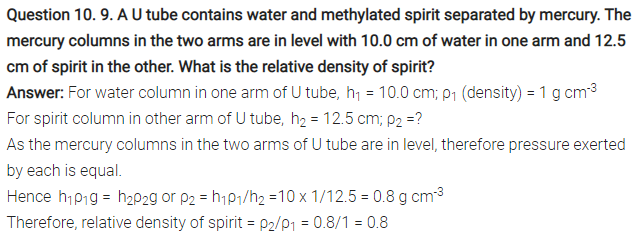
Question 10. 10. In Q.9, if 15.0 cm of water and spirit each are further poured into the respective arms of the tube, what is the difference in the levels of mercury in the two arms? (Relative density of mercury = 13.6)
Answer:
Height of the water column, h1 = 10 + 15 = 25 cm
Height of the spirit column, h2 = 12.5 + 15 = 27.5 cm
Density of water, ρ1 = 1 g cm–3
Density of spirit, ρ2 = 0.8 g cm–3
Density of mercury = 13.6 g cm–3
Let h be the difference between the levels of mercury in the two arms.
Pressure exerted by height h, of the mercury column:
= hρg
= h × 13.6g … (i)
Difference between the pressures exerted by water and spirit:
= ρ1h1g – ρ2h2g
= g(25 × 1 – 27.5 × 0.8)
= 3g … (ii)
Equating equations (i) and (ii), we get:
13.6 hg = 3g
h = 0.220588 ≈ 0.221 cm
Hence, the difference between the levels of mercury in the two arms is 0.221 cm.

Question 10. 13. Glycerine flows steadily through a horizontal tube of length 1.5 m and radius 1.0 cm. If the amount of glycerine collected per second at one end is 4.0 x 10-3 kg s-1, what is the pressure difference between the two ends of the tube? (Density of glycerine = 1.3 x 103 kg m-3 and viscosity of glycerine = 0.83 Pa s). [You may also like to check if the assumption of laminar flow in the tube is correct],
Answer:



Answer: Figure (a) is incorrect. It is because of the fact that at the kink, the velocity of flow of liquid is large and hence using the Bernoulli’s theorem the pressure is less. As a result, the water should not rise higher in the tube where there is a kink (i.e., where the area of cross-section is small).


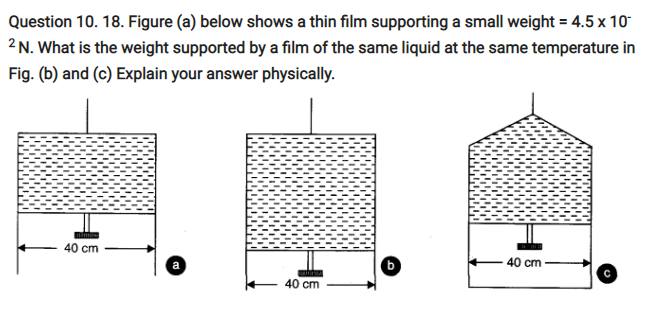
Ans. (a) Here, length of the film supporting the weight = 40 cm = 0.4 m. Total weight supported (or force) = 4.5 x 10-2 N.
Film has two free surfaces, Surface tension, S =4.5 x 10-2/2 x 0.4 =5.625 x 10-2 Nm-1
Since the liquid is same for all the cases (a), (b) and (c), and temperature is also same, therefore surface tension for cases (b) and (c) will also be the same = 5.625 x 10-2. In Fig. 7(b), 38(b) and (c), the length of the film supporting the weight is also the saihe as that of (a), hence the total weight supported in each case is 4.5 x 10-2 N.

Question 10. 20. What is the excess pressure inside a bubble of soap solution of radius 5.00 mm, given that the surface tension of soap solution at the temperature (20 °C) is 2.50 x 10-2 Nm-1? If an air bubble of the same dimension were formed at depth of 40.0 cm inside a container containing the soap solution (of relative density 1.20), what would be the pressure inside the bubble? (1 atmospheric pressure is 1.01 x 105 Pa).
Answer: Here surface tension of soap solution at room temperature
T = 2.50 x 10-2 Nm-1, radius of soap bubble, r = 5.00 mm = 5.00 x 10-3 m.


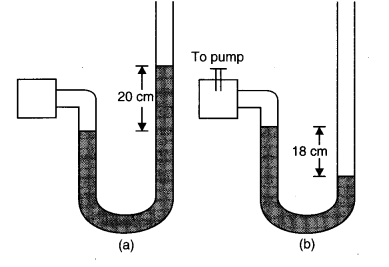
Question 10. 22. A manometer reads the pressure of a gas in an enclosure as shown in Fig. (a) When a pump removes some of the gas, the manometer reads as in Fig. (b). The liquid used in the manometers is mercury and the atmospheric pressure is 76 cm of mercury.
(a) Give the absolute and gauge pressure of the gas in the enclosure for cases (a) and (b), in units of cm of mercury.
(b) How would the levels change in case (b) if 13.6 cm of water (immiscible with mercury) is poured into the right limb of 1 the manometer? Ignore the small change in the volume of the gas.


Question 10. 24. During blood transfusion, the needle is inserted in a vein where the gauge pressure is 2000 Pa. At what height must the blood container be placed so that blood may just enter the vein? Given: density of whole blood = 1.06 x 103 kg m-3.
Answer: h=P/ρg =200/(1.06 x 103 x 9.8) =0.1925 m
The blood may just enter the vein if the height at which the blood container be kept must be slightly greater than 0.1925 m i.e„ 0.2 m.
Question 10. 25. In deriving Bernoulli’s equation, we equated the work done on the fluid in the tube to its change in the potential and kinetic energy, (a) What is the largest average velocity of blood flow in an artery of diameter 2 x 10-3 m if the flow must remain laminar? (b) Do the dissipative forces become more important as the fluid velocity increases? Discuss qualitatively.
Answer: (a) If dissipative forces are present, then some forces in liquid flow due to pressure difference is spent against dissipative forces, due to which the pressure drop becomes large.
(b) The dissipative forces become more important with increasing flow velocity, because of turbulence.






where ρ0 = 1.25 kg m-3 is the density at sea level, and y0 is a constant. This density variation is called the law of atmospheres. Obtain this law assuming that the temperature of atmosphere remains a constant (isothermal conditions). Also, assume that the value of g remains constant.
(b) A large He balloon of volume 1425 m3 is used to lift a payload of 400 kg. Assume that the balloon maintains a constant radius as it rises. How high does it rise?[Take y0 = 8000 m and ρHe = 0.18 kg m-3].
Answer: (a) We know that rate of decrease of density p of air is directly proportional to the height y. It is given as dρ/dy = – ρ/y0
where y is a constant of proportionality and -ve sign signifies that density is decreasing with increase in height. On integration, we get

