Variation of pressure with depth
- Consider a cylindrical object inside a fluid;consider 2 different positions for this object.
- Fluid is at rest therefore the force along the horizontal direction is 0.
- Forces along the vertical direction:-
- Consider two positions 1 and 2.
- Force at position 1 is perpendicular to cross sectional area A, F1= P1
- Similarly F2=P2
- Total force Fnet= -F1+F2 as F1 is along negative y axis therefore it is –ive. And F2 is along +ive y -axis.
- Fnet =(P2-P1)A
- This net force will be balanced by the weight of the cylinder(m).
- Therefore under equilibrium condition
- Fnet=mg=weight of the cylinder = weight of the fluid displaced.
- =ρ Vg where ρ=density=volume of the fluid
- =ρhAg where V=hA(h=height and A= area)
- Therefore (P2-P1) A=ρhAg
- P2-P1 = ρhg,Therefore the difference in the pressure is dependent on height of the cylinder.
- Consider the top of the cylinder exposed to air therefore P1=Pa(where Pa= P1 is equal to atmospheric pressure.)
- Then P2=Pa+ ρhg
- Conclusion: The pressure P, at depth below the surface of a liquid open to the atmosphere is greater than atmospheric pressure by an amount ρhg.
- The pressure is independent of the cross sectional or base area or the shape of the container.

Problem:- What is the pressure on aswimmer 10 m below the surface of a lake?
Answer:-
Here, h = 10 m and ρ = 1000 kg m-3. Take g = 10 m s–2
P = Pa + ρgh
= 1.01 × 105 Pa + 1000 kg m–3 × 10 m s–2 × 10 m
= 2.01 × 105 Pa
≈ 2 atm
This is a 100% increase in pressure fromsurface level. At a depth of 1 km the increase in
Pressure is 100 atm! Submarines are designedto withstand such enormous pressures.
Problem:- A vertical off-shore structure is built to withstand a maximum stress of 109 Pa. Is the structure suitable for putting up on top of an oil well in the ocean? Take the depth of the ocean to be roughly 3 km, and ignore ocean currents.
Answer:- Yes
The maximum allowable stress for the structure, P = 109 Pa
Depth of the ocean, d = 3 km = 3 × 103 m
Density of water, ρ = 103 kg/m3
Acceleration due to gravity, g = 9.8 m/s2
The pressure exerted because of the sea water at depth, d = ρdg
= 3 × 103 × 103 × 9.8 = 2.94 × 107 Pa
The maximum allowable stress for the structure (109 Pa) is greater than the pressure of the sea water (2.94 × 107 Pa). The pressure exerted by the ocean is less than the pressure that the structure can withstand. Hence, the structure is suitable for putting up on top of an oil well in the ocean.
Hydrostatic Paradox
- Hydrostatic Paradox means: – hydro = water, static =at rest
Paradox meansthat something taking place surprisingly.
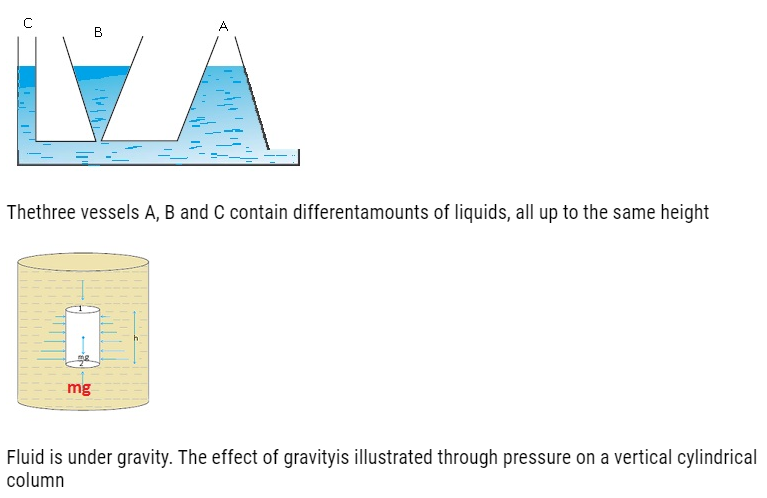
- Consider 3 vessels of very different shapes (like thin rectangular shape, triangular and some filter shape) and we have a source from which water enters into these 3 vessels.
- Water enters through the horizontal base which is the base of these 3 vessels we observe that the level of water in all the 3 vessels is same irrespective of their different shapes.
- This is because pressure at some point at the base of these 3 vessels is same.
- The water will rise in all these 3 vessels till the pressure at the top is same as the pressure at the bottom.
- As pressure is dependent only on height therefore in all the 3 vessels the height reached by the water is same irrespective of difference in their shapes.
- This experiment is known as Hydrostatic Paradox.