Anomalous Behaviour of Water
- Water shows some exceptional behaviour that is when it is heated at 0°C, it contracts instead of expandingand it happens till it reaches 4 °C. The volume of a given amount of water is minimumat 4 °C therefore its density is maximum(Refer the Fig). After 4 °C water starts expanding. Below 4 °C, the volume increases, and therefore the density decreases. This means water has maximum density at 4 °C.
- Advantages of Anomalous behaviour of Water
- Because of this property of water in lakes and ponds freeze only at the top layer and at the bottom it does not, butif the water freezes at the bottom also then animal and plant life would not be possible.
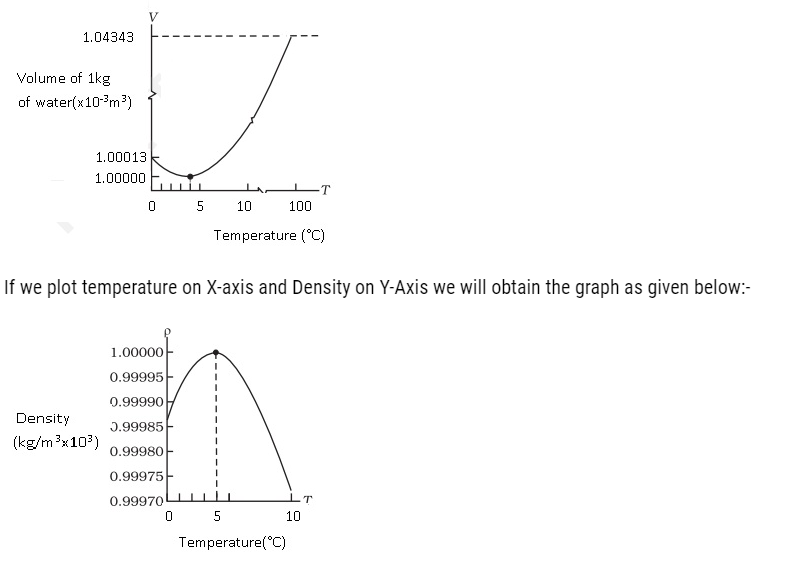
The information we get from the above graph means that the density increases as its temperature rises from 0°C to 4 °C and density decreases after 4°C.

By solving we get ΔV= 3l2Δl(we are neglecting (Δl)2 and (Δl)3as they are very small as to compared to l.
Therefore, Δ V = (3V Δl)/l
=3VαlΔT
Which gives αv = 3αl the relation between coefficient of volume expansion and coefficient of linear expansion.
Thermal stress: ( Thermal Properties of Matter )
- Mechanical stress induced by a body when some or all of its parts are not free to expand or contract in response to change in temperature.
- When an object is heated or cooled either it expands or it contracts but if for some reason if the object is not allowed to expand to contract under that case mechanical stress is induced in the body which is known as Thermal Stress.
- Example :-
While designing structures like concrete highways gaps are left which are filled by some flexible material so that concrete is allowed to expand or contract.
Heat Capacity ( Thermal Properties of Matter )
The change in temperature of a substance, when a given quantity of heat is absorbed or rejected by substance is characterised by a quantity called the heat capacity of that substance.
- It is denoted by S.
- It is given as S = ΔQ/ ΔT
Where ΔQ = amount of heat supplied to the substance and T to T + ΔT change in its temperature.


Molar specific heat capacity: –
- Heat capacity per mole of the substance is the defined as the amount of heat (in moles) absorbed or rejected(instead of mass m in kg) by the substance to change its temperature by one unit.
Mathematically can be written as:-
C = S/ μ= ΔQ / μ ΔT
Where
- μ= amount of substance in moles
- C = molar specific heat capacity of the substance.
- ΔQ = amount of heat absorbed or rejected by a substance.
- ΔT = temperature change
It depends on the nature of the substance and its temperature. The SI unit of molar specific heat capacity is Jmol–1 K–1
Molar specific heat capacity (Cp):-
- If the gas is held under constant pressure during the heat transfer, then the corresponding molar specific heat capacity is called molar specific heat capacity at constant pressure (Cp).
Molar specific heat capacity (Cv):-
- If the volume of the gas is maintained during the heat transfer, then the corresponding molar specific heat capacity is called molar specific heat capacity at constant volume (Cv).
- Water has highest specific heat of capacity because of which it is used as a coolant in automobile radiators and in hot water bags.

Solution:- Mass of the metal, m = 0.20 kg = 200 g
Initial temperature of the metal, T1 = 150°C
Final temperature of the metal, T2 = 40°C
Calorimeter has water equivalent of mass, m’ = 0.025 kg = 25 g
Volume of water, V = 150 cm3
Mass (M) of water at temperature T = 27°C: 150 × 1 = 150 g
Fall in the temperature of the metal:
ΔT = T1 – T2 = 150 – 40 = 110°C
Specific heat of water, Cw = 4.186 J/g/°K
Specific heat of the metal = C
Heat lost by the metal, θ = mCΔT … (i)
Rise in the temperature of the water and calorimeter system:
ΔT = 40 – 27 = 13°C
Heat gained by the water and calorimeter system:
Δθ’’ = m1 CwΔT’
= (M + m′) Cw ΔT’ … (ii)
Heat lost by the metal = Heat gained by the water and calorimeter system
mCΔT = (M + m’) Cw ΔT’
200 × C × 110 = (150 + 25) × 4.186 × 13
