Introduction

In this chapter we will learn about oscillatory motion or oscillations. Any motion which repeats itself at regular intervals of time is known as periodic motion. If a body moves back and forth repeatedly about its mean position then it is said to be in oscillatory motion.

For example: The to and fro movement of pendulum, jumping on a trampoline, a child swinging on a swing.

Oscillations can be defined as Periodic to and fro motion which repeat itself at regular intervals of time.

Periodic and Oscillatory motions

Oscillations are defined as to and fro motion which repeat itself after regular intervals of time.In oscillations, the frequency of vibrations iscomparatively less. 

For example: The to and fro motion of a pendulum clock

Frequency

It is defined as number of cycles per second.

• It is denoted by ν.
• I.unit is sec^-1
• Special Unit is Hertz(Hz)

Problem: – On an average human heart is found to be beat 75 times in a minute. Calculate frequency and time period?

Answer: –

The beat frequency of heart = 75/ (1 min)

 = 75/ (60 s)

 = 1.25 s^–1

 = 1.25 Hz

 The time period T = 1/ (1.25 s^–1) = 0.8 s 

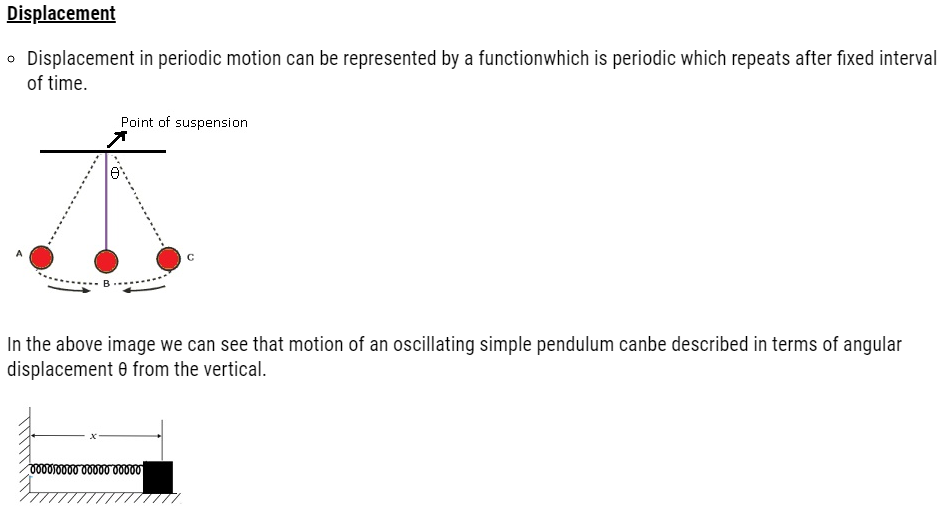
In the above image we can see that there is a block whose one end is attached to a spring and another is attached to a rigid wall.x is the displacement from the wall.

In the above figure a blockis attached to a spring, the other end of which is fixed to a rigid wall. The block moves on a frictionless surface. The motion of the block can be described in terms of its distance or displacement x from the wall.

f (t) = A cos ωt

As cosine function repeats after 2π so it can be written as

cos (θ) = cos (ωt + 2π)            Equation (1)

cos (ωt) = cos (ωt + 2π) (it keep on repeating after 2π)

Let Time Period = T

f (T) = f(t+T) where displacement keeps on repeating after (t+T)

Acos (ωt) = cosω(t+T) = Acos (ωt+ wT)

Acosωt = A cos (ωt+ωT)          Equation (2)

From Equation (1) and Equation (2)

ωT= 2π

Or T=2π /ω

Displacement as a combination of sine and cosine functions

f (t) = A cos ωt

f (t) = A sin ωt

f (t) = A sin ωt + A cos ωt

LetA = D cosΦ              Equation (3)

B=DsinΦEquation (4)

f (t) =DcosΦ sinωT + DsinΦ cos ωt

D (cosΦ sinωT + sinΦ cos ωt)

(Using sinAcosB + sinBcosA = sin (A+B))

Therefore we can write

f (T)= D sin (ωT+Φ)

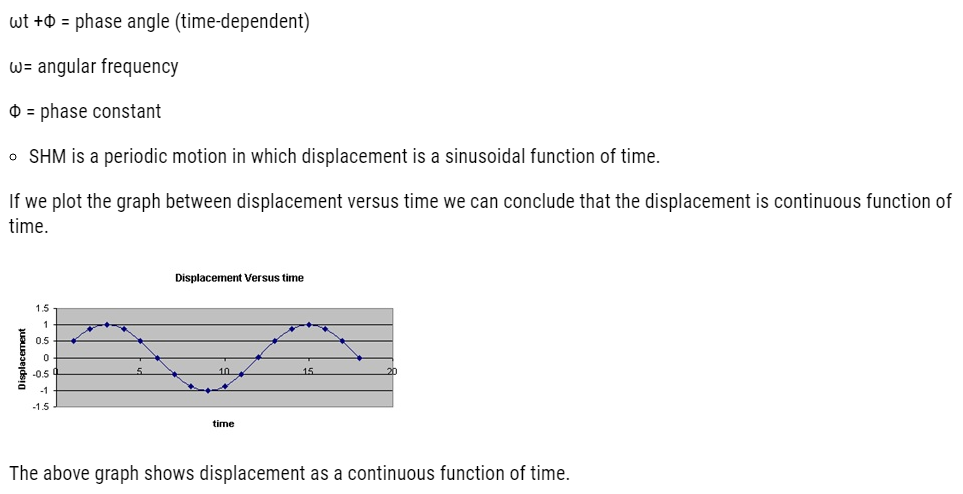
From the above expression we can say displacement can be written as sine and cosine functions.

D in terms of A and B:-

A² B² = D²sin² Φ + D²cos² Φ

A² B² = D²

Or D= AB

Φ In terms of A and B

Dividing Equation (4) by (3)

B/A= DsinΦ/Dcos Φ

tan Φ = B/A

Or Φ= tan^-1 B/A

Problem:-Which of the followingfunctions of time represent (a) periodic and (b) non-periodic motion? Give the period foreach case of periodic motion [ω is anypositive constant].

(i) sin ωt + cos ωt

(ii) sin ωt + cos 2 ωt + sin 4 ωt

(iii) e–ωt

(iv) log (ωt)

 Answer:-

• sin ωt + cos ωt is a periodic function, it can also be written as

 2 sin (ωt + π/4).

Now 2 sin (ωt + π/4)= 2 sin (ωt + π/4+2π)

= 2 sin [ω (t + 2π/ω) + π/4]

The periodic time of the function is 2π/ω.

(ii) This is an example of a periodic motion. Itcan be noted that each term represents aperiodic function with a different angularfrequency. Since period is the least intervalof time after which a function repeats itsvalue, sin ωt has a period T₀= 2π/ω; cos 2 ωt

has a period π/ω =T₀/2; and sin 4 ωt has aperiod 2π/4ω = T₀/4. The period of the firstterm is a multiple of the periods of the last

two terms. Therefore, the smallestintervalof time after which the sum of the threeterms repeats is T₀, and thus the sum is aperiodic function with aperiod 2π/ω.

(iii) The function e^–ωt is not periodic, itdecreases monotonically with increasingtime and tends to zero as t →∞ and thus,never repeats its value.

(iv) The function log (ωt) increases monotonicallywith time t. It, therefore, neverrepeats its value and is a non-periodicfunction. It may be noted that as t →∞,log (ωt) diverges to ∞. It, therefore, cannot represent any kind of displacement.

Phase

It is that quantity that determines the state of motion of the particle.

• Its value is (ωt + Φ)
• It is dependent on time.

Value of phase at time t=0, is termed as Phase Constant. When the motion of the particle starts it goes to one of the extreme position at that time phase is considered as 0.

Let x (t) = A cos (ωt) where we are taking (Φ = 0)

1. Mean Position (t= 0)
2. x (0) = A cos (0) = A (cos0=1)
3. t=T/4, t= T/2, t=3T/4, t=T and t=5T/4

Answer:

In SHM, acceleration a is related to displacement by the relation of the form

 a = -kx, which is for relation (c).

Problem: – The motion of a particle executing simple harmonic motion is described by the displacement function,

x (t) = A cos (ωt + φ).

If the initial (t = 0) position of the particle is 1 cm and its initial velocity is ω cm/s, what are its amplitude and initial phase angle? The angular frequency of the particle is π s^–1. If instead of the cosine function, we choose the sine function to describe the SHM: x = B sin (ωt + α), what are the amplitude and initial phase of the particle with the above initial conditions.

Answer:-

Initially, at t = 0;

Displacement, x = 1 cm

Initial velocity, v = ω cm/ sec.

Angular frequency, ω = π rad/s^–1

It is given that,

x (t) = A cos (ωt + Φ)

1 = A cos (ω × 0 + Φ) = A cos Φ

A cosΦ = 1                          … (i)

Velocity, v= dx/dt

ω = -A ω sin (ωt + Φ)

1 = -A sin (ω × 0 + Φ) = -A sin Φ

A sin Φ = -1                         … (ii)

Squaring and adding equations (i) and (ii), we get:

A² (sin² Φ + cos² Φ) = 1 + 1

A² = 2

∴ A = √2 cm

Dividing equation (ii) by equation (i), we get:

tan Φ = -1

∴Φ = 3π/4, 7π/4…

SHM is given as:

x = B sin (ωt + α)

Putting the given values in this equation, we get:

1 = B sin [ω × 0 + α] = 1 + 1

B sin α = 1                           … (iii)

Velocity, v = ω B cos (ωt + α)

Substituting the given values, we get:

π = π B sin α

B sin α = 1                            … (iv)

Squaring and adding equations (iii) and (iv), we get:

B2 [sin2 α + cos2 α] = 1 + 1

B2 = 2

∴ B = √2 cm

Dividing equation (iii) by equation (iv), we get:

B sin α / B cos α = 1/1

tan α = 1 = tan π/4

∴α = π/4, 5π/4…

Angular Frequency (ω)

Angular frequency refers to the angular displacement per unit time. It can also be defined as the rate of change of the phase of a sinusoidal waveform (e.g., in oscillations and waves). Angular frequency is larger than frequency ν (in cycles per second, also called Hz), by a factor of 2π.

Consider the oscillatory motion which is varying with time t and displacement x of the particle from the origin:

x (t) = cos (ωt + Φ)

Let Φ = 0

x (t) = cos (ωt)

After t=T i.e. x (t) = x (t+T)

A cos ωt = A cos ω (t + T)

Now the cosine function is periodic with period 2π, i.e., it first repeats itself after 2π. Therefore,

ω (t + T) = ωt + 2π

i.e. ω = 2π/ T

Where ω = angular frequency of SHM.

• I. unit is radians per second.
• It is 2π times the frequency of oscillation.
• Two simple harmonic motions may have the same A and φ, but different ω.

Problem: – Which of the following functions of time represent (a) simple harmonic, (b) periodic but not simple harmonic, and (c) non-periodic motion? Give period for each case of periodic motion (ω is any positive constant):

(a) sin ωt – cos ωt

(b) sin3ωt

(c) 3 cos (π/4 – 2ωt)

(d) cos ωt + cos 3ωt + cos 5ωt

(e) exp (–ω²t²)

Answer: –

(a) SHM

The given function is:

sinωt – cos ωt

This function represents SHM as it can be written in the form: a sin (ωt + Φ)

Its period is: 2π/ω

(b) Periodic but not SHM

The given function is:

sin 3ωt = 1/4 [3 sin ωt – sin3ωt]

The terms sin ωt and sin ωt individually represent simple harmonic motion (SHM). However, the superposition of two SHM is periodic and not simple harmonic.

Its period is: 2π/ω

(c) SHM

The given function is:

This function represents simple harmonic motion because it can be written in the form: a cos (ωt + Φ) its period is: 2π/2ω = π/ω

(d) Periodic, but not SHM

The given function is cosωt + cos3ωt + cos5ωt. Each individual cosine function represents SHM. However, the superposition of three simple harmonic motions is periodic, but not simple harmonic. 

(e) Non-periodic motion

The given function exp (-ω²t²) is an exponential function. Exponential functions do not repeat themselves. Therefore, it is a non-periodic motion.

 (f) The given function 1 + ωt + ω²t² is non-periodic.

Problem: Which of the followingfunctions of time represent (a) simple harmonic motion and (b) periodic but notsimple harmonic? Give the period for each case?

(1) sin ωt – cos ωt

(2) sin² ωt

Answer:

(a) sin ωt – cos ωt

= sin ωt – sin (π/2 – ωt)

= 2 cos (π/4) sin (ωt – π/4)

 = √2 sin (ωt – π/4)

This function represents a simple harmonicmotion having a period T = 2π/ω and aphase angle (–π/4) or (7π/4).

(b) sin² ωt

= ½ – ½ cos 2 ωt

The function is periodic having a period T = π/ω. It also represents a harmonic motion with the point of equilibrium occurring at ½ instead of zero.