Friction

• Friction is a contact force that opposes relative motion.
• No friction exists till an external force is applied.

There are 3 types of Friction:

• Static friction
  • Force that resists initiation of motion of one body over another with which it is in contact
  • Opposes Impending motion
  • Denoted by f_s  

Let the ball be at rest initially

Applied force, F_a = 0; Static friction, f_s = 0

f_s acts when a body is at rest. Hence called Static friction

• Limiting value of f_s depends on Normal reaction, and is independent of the area of contact

f_s max ∝ N

f_s max = constant * N

f_s max = μ_s N

where μ_s is the coefficient of static friction

This coefficient depends on the nature of surfaces in contact.

• According to the Law of Static friction, Static friction is always less than or equal to the limiting value of f_s

  f_s  =< f_s max 

  f_s max = μ_s N 

  f_s  =< μ_s N

Kinetic friction

• Force that resists motion of one body over another with which it is in contact.
• Denoted by f_k
• As motion starts, f_s vanishes and f_k appears

(F_a – f_k) = ma

a = (F_a – f_k)/m

2. When applied force = f_k

F_a = f_k

Therefore, a = 0 i.e. the body moves with uniform velocity

3. When applied force = 0

F_a = 0

A = -f_k/m

No motion occurs, the body stops

Relation between Coefficient of Static & Kinetic friction

f_k = μ_k N

f_s =< μ_s N

f_s > f_k (to keep the body moving)

μ_s N > μ_k N

Or,   μ_{k  <}  μ_s

Coefficient of kinetic friction is smaller than the coefficient of static friction.

Problem: Calculate the force required for pushing a  30 kg wooden bar  over a wooden floor at a constant speed. Coefficient of friction of wood over wood = 0.25

Solution.

M = 30 kg

μ = 0.25

(F_a – f) = ma

For constant speed, a = 0

So, F_a = f= μN

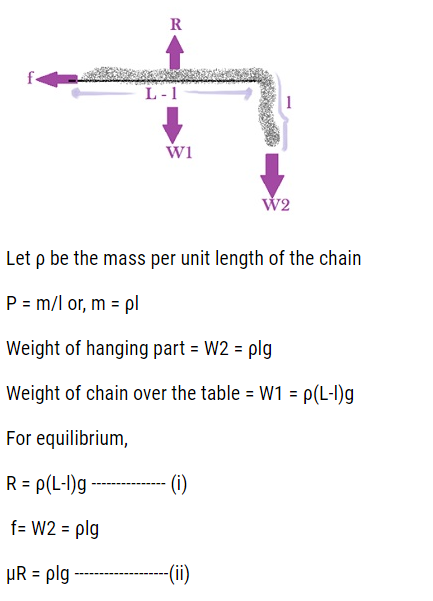
(i)Divided by (ii) gives

1/μ = (L-l)/l

l = μL – μl

l + μl = μL

Therefore, l = μL/( μ + 1)