Dynamics of Rotational Motion about a Fixed Axis
- Only those components of torques, which are along the direction of the fixed axis, need to be considered because the component of the torque perpendicular to the axis of rotation will tend to turn the axis from its position.
- This means
- We need to consider only those forces that lie in planes perpendicular to the axis. Forces which are parallel to the axis will give torques perpendicular to the axis.
- We need to consider only those components of the position vectors which are perpendicular to the axis. Components of position vectors along the axis will result in torques perpendicular to the axis


Example – Torques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. Which of the two will acquire a greater angular speed after a given time?
Solution: We know that t = I∝, since torque is equal so
(I∝)cylinder = (I∝)sphere
Isphere = 2/5 MR2 & Icylinder = MR2
∝cylinder < ∝sphere




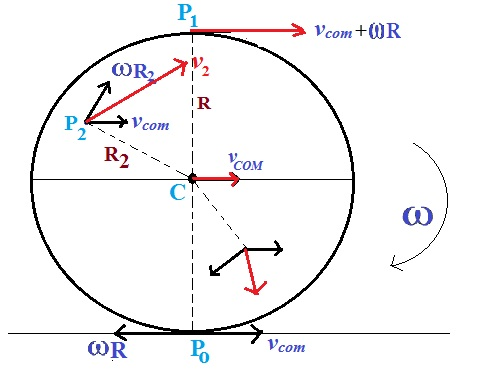
- Here in the figure we can see that every point have two velocities, one in the direction of velocity of COM and other perpendicular to the line joining centre and the point.
- Point Po have opposite velocities , and if condition of no-slipping is there then it must have zero velocity, so Vcom = ω R
- At point P1 both the velocities add up.
- At any other point, add both the velocities vectorially to get the resultant, which are shown for some of the cases in red color in figure.
- The line passing through PO and parallel to w is called the instantaneous axis of rotation.
- The point PO is instantaneously at rest.
- Kinetic Energy of Rolling Motion
- KErolling = KEtranslation + KErotation

