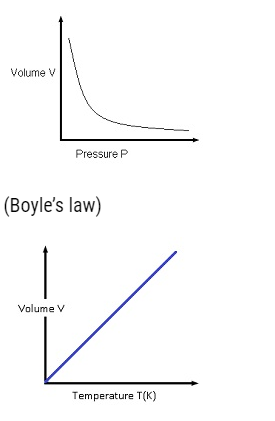
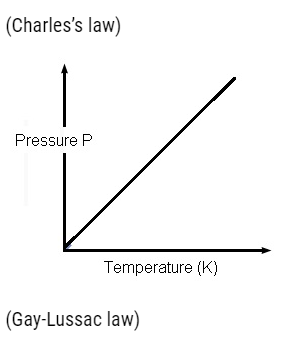
Perfect Gas Equation

• Perfect gas equation is given by PV=μRT,
  • WhereP,V are pressure, volume, T =absolute temperature,μ = number of moles and R =universal gas constant.
  • R= k_BN_A where k_B = Boltzmann constant and N_A = Avogadro’s Number
• This equation tells about the behaviour of gas at a particular situation.
• If a gas satisfies this equation then the gas is known as Perfect gas or an ideal gas.

Different Forms of Perfect Gas Equation

1. PV=μRT (i)

• Where μ (no. of moles) = N/N_A where N=no of molecules and N_A = Avogadro number(no of molecules in 1 mole of gas).Orμ = M/M_owhere M=mass of sample of gas and M_o = molar mass.
• PV = (N/N_A)RT(putting μ=N/N_A in equation(i))
• By simplifying PV = Nk_BT
• PV=Nk_BT => P = (N/V) k_BT => P=nk_BT where n(number density) =N/V where N=number of molecules and V=volume.
• Therefore we get PV=nk_BT

2. Substitute μ = M/M_o in equation(i)

• PV=(M/M_o) RT => P=(M/V)1/M_oRT where
  • ρ(mass density of the gas) = M/V
• Therefore P=ρRT/M_o

Ideal Gas

• A gas that satisfies the perfectgas equation exactly at all pressures and temperatures.
• Ideal gas is atheoretical concept.
• No real gas is truly ideal.A gas which is ideal is known as real gas.
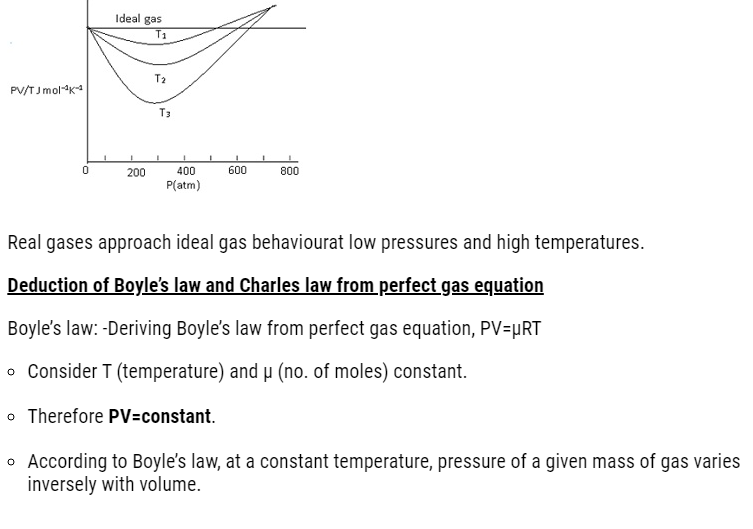
• Real gases approach the ideal gas behaviour for low pressures and high temperatures.

Problem:- ( Kinetic Theory Notes )

Estimate the total number of air molecules (inclusive of oxygen, nitrogen, water vapour

and other constituents) in a room of capacity 25.0 m³ at a temperature of 27 °C and 1 atm

pressure.

Answer:-

Volume of the room, V = 25.0 m³

Temperature of the room, T = 27°C = 300 K

Pressure in the room, P = 1 atm = 1 × 1.013 × 10⁵ Pa

The ideal gas equation relating pressure (P), Volume (V), and absolute temperature (T)

can be written as:

PV = k_BNT

Where,

K_B is Boltzmann constant = 1.38 × 10^–23 m² kg s^–2 K^–1

N is the number of air molecules in the room

N=PV/ K_BT

=1.013×10⁵x25/1.38×10^-23x300

= 6.11 × 10²⁶ molecules

Therefore, the total number of air molecules in the given room is 6.11 × 10²⁶

Real gases deviation from ideal gas

• Real gases approach the ideal gas behaviour for low pressures and high temperatures.
• Ideal gas equation PV=μRT, for 1 mole ,μ=1,PV=RT
• =>PV/RT=constant
• Graph should be a straight line(parallel to x-axis) for ideal gas.
• This means it has constant value at all temperature and all pressure.

But in case of real gases graph approach ideal gas behaviour at high temperature and low pressure.

• At high temperature and low pressure molecules are far apart. When temperature is increased the molecules will move randomly far from each other.
• As a result molecular interaction decreases the gas behaves as an ideal gas.
• The ideal behaviour comes into picture when the molecular present inside the gas don’t interact with each other.

Charles’s law:-Consider If P(Pressure) is constant, then