NCERT Solutions for Class 11 Physics Chapter 14 Oscillations
QUESTIONS FROM TEXTBOOK ( Oscillations Notes )
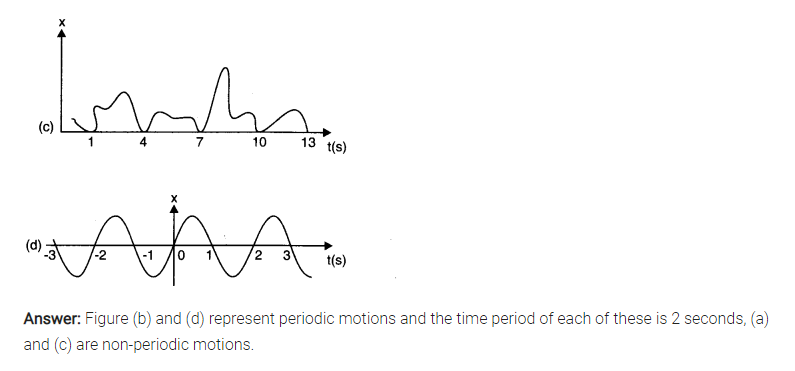
Question 14. 1. Which of the following examples represent periodic motion?
(a) A swimmer completing one (return) trip from one bank of a river to the other and back.
(b) A freely suspended bar magnet displaced from its N-S direction and released.
(c) A hydrogen molecule rotating about its centre of mass.
(d) An arrow released from a bow.
Answer: (a) It is not a periodic motion. Though the motion of a swimmer is to and fro but will not have a definite period.
(b) Since a freely suspended magnet if once displaced from N-S direction and released, it oscillates about this position, it is a periodic motion.
(c) The rotating motion of a hydrogen molecule about its centre of mass is periodic.
(d) Motion of an arrow released from a bow is non-periodic.
Question 14. 2. Which of the following examples represent (nearly) simple harmonic motion and which represent
periodic but not simple harmonic motion?
(a) the rotations of earth about its axis.
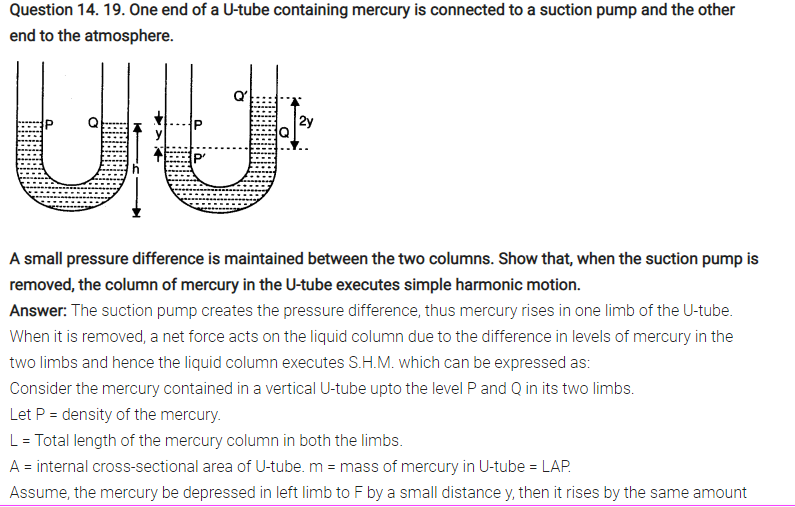
(b) motion of an oscillating mercury column in a U-tube.
(c) motion of a ball bearing inside a smooth curved bowl, when released from a point slightly above the lowermost point.
(d) general vibrations of a polyatomic molecule about its equilibrium position.
Answer: (a) Since the rotation of earth is not to and fro motion about a fixed point, thus it is periodic but not S.H.M.
(b) It is S.H.M.
(c) It is S.H.M.
(d) General vibrations of a polyatomic molecule about its equilibrium position is periodic but non SHM. In fact, it is a result of superposition of SHMs executed by individual vibrations of atoms of the molecule.



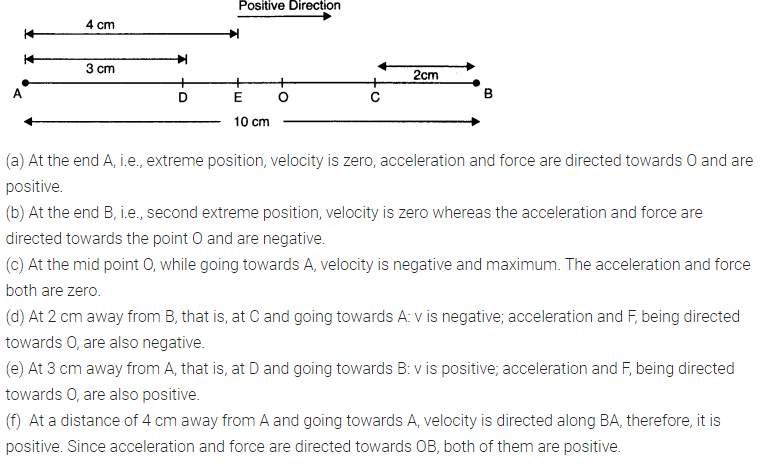
Question 14. 5. A particle is in linear simple harmonic motion between two points, A and B, 10 cm apart. Take the direction from A to B as the positive direction and give the signs of velocity, acceleration and force on the particle when it is
(a) at the end A,
(b) at the end B,
(c) at the mid-point of AB going towards A,
(d) at 2 cm away from B going towards A,
(e) at 3 cm away from A going towards B, and (f) at 4 cm away from B going towards A.
Answer: In the fig. (given below), the points A and B, 10 cm apart, are the extreme positions of the particle in SHM, and the point O is the mean position. The direction from A to B is positive, as indicated.
Question 14. 6. Which of the following relationships between the acceleration a and the displacement x of a particle involve simple harmonic motion?
(a) a = 0.7x (b) a = – 200 x2
(c) a = – 10x (d) a = 100 x3
Answer: Only (c) i.e., a = – 10x represents SHM. This is because acceleration is proportional and opposite to displacement (x).

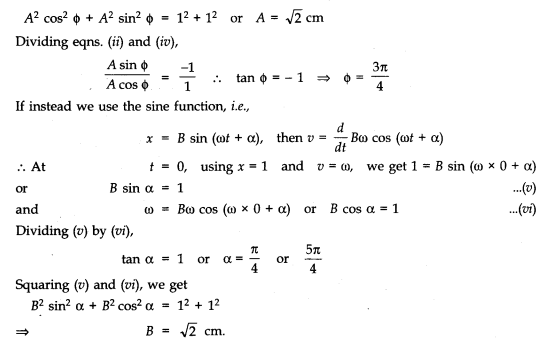




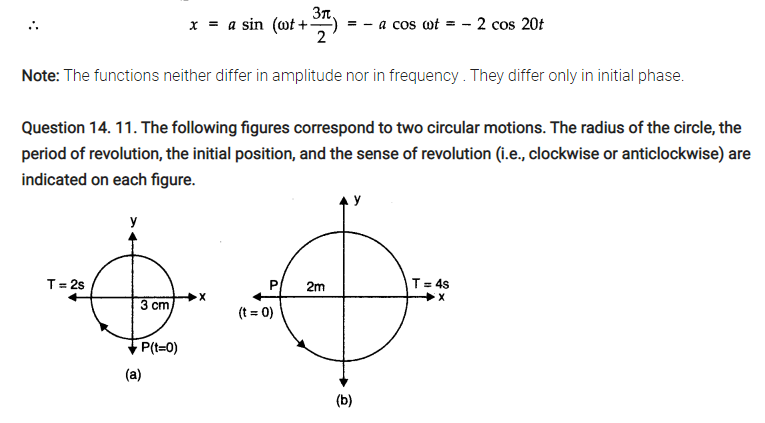
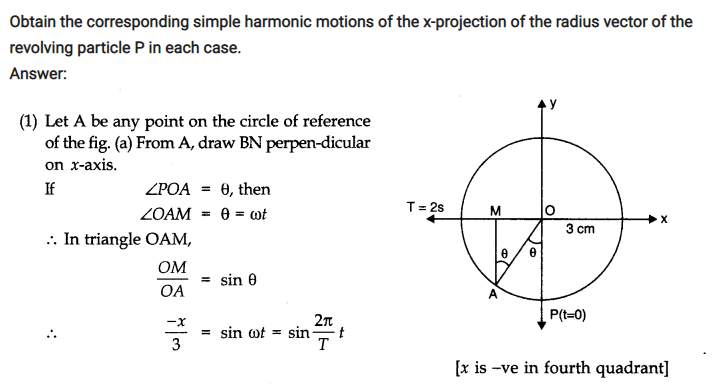
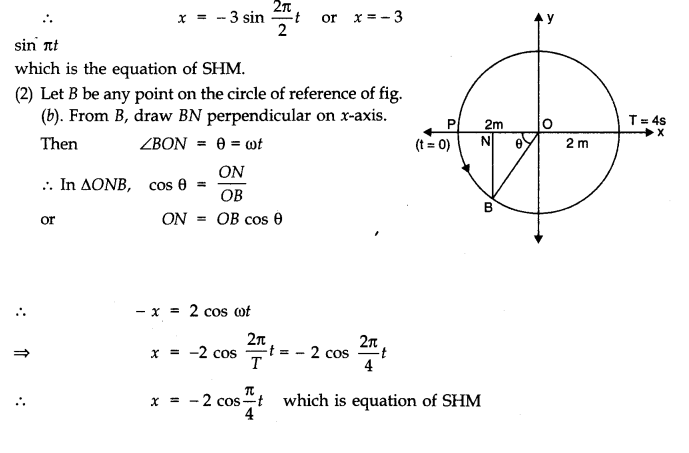
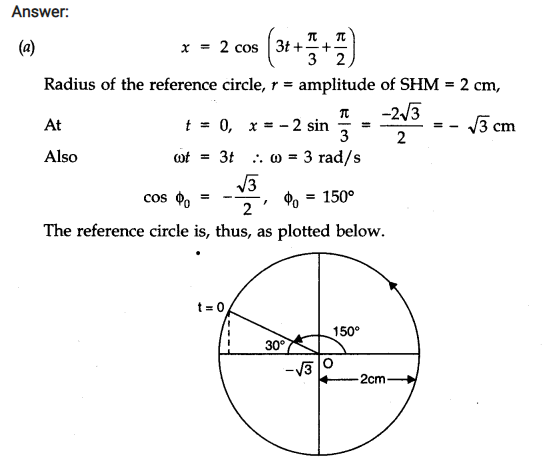
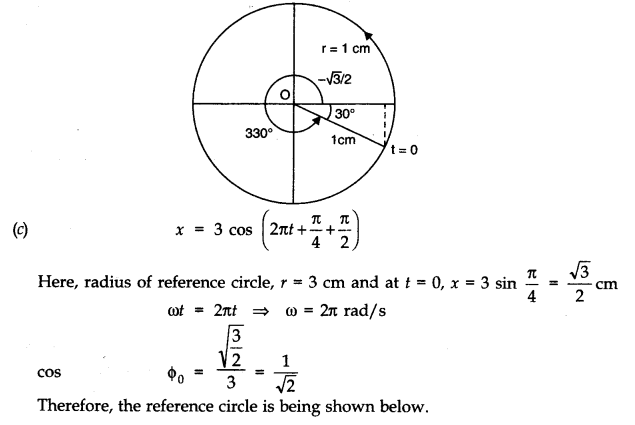
Question 14. 12. Plot the corresponding reference circle for each of the following simple harmonic motions. Indicate the initial (t = 0) position of the particle, the radius of the circle, and the angular speed of the rotating particle. For simplicity, the sense of rotation may be fixed to be anti-clockwise in every case:
(x is in cm and t is in s)
(a) x = – 2 sin (3t + π /3)
(b) x = cos (π /6 – t)
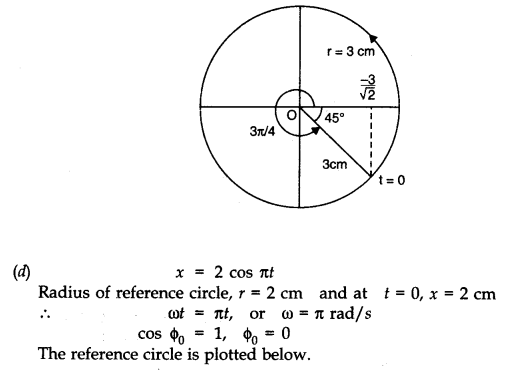
(c) x = 3 sin (2πt + π /4)
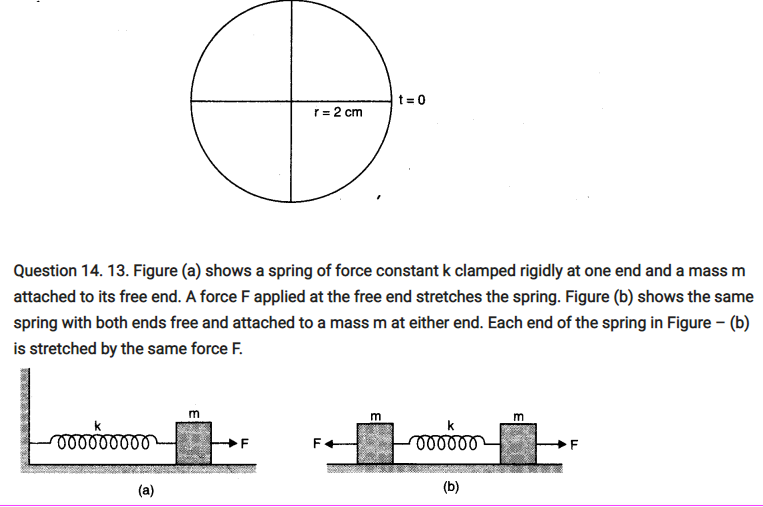
(d) x = 2 cos π t.








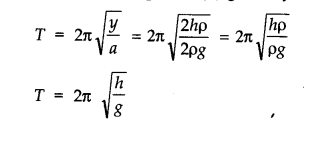
Question 14. 20. An air chamber of volume V has a neck area of cross-section into which a ball of mass m just fits and can move up and down without any friction (Fig.). Shaw that when the ball is pressed down a little and released, it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal.









