Bernoulli’s Principle

• For a streamline fluid flow, the sum of the pressure (P), the kinetic energy per unit volume (ρv²/2) and the potential energy per unit volume (ρgh) remain constant.
• Mathematically:- P+ ρv²/2 + ρgh = constant
  • where P= pressure ,
  • E./ Volume=1/2mv²/V = 1/2v²(m/V) = 1/2ρv²
  • E./Volume = mgh/V = (m/V)gh = ρgh

Derive: Bernoulli’s equation

Assumptions:

1. Fluid flow through a pipe of varying width.
2. Pipe is located at changing heights.
3. Fluid is incompressible.
4. Flow is laminar.
5. No energy is lost due to friction:applicable only to non-viscous fluids.

• Mathematically: –
• Consider the fluid initially lying between B and D. In an infinitesimal timeinterval Δt, this fluid would have moved.
  • Suppose v₁= speed at B and v₂= speedat D, initial distance moved by fluid from to C=v₁Δt.
  • In the same interval Δtfluid distance moved by D to E = v₂Δt.
  • P₁= Pressureat A_1, P₂=Pressure at A₂.
  • Work done on the fluid atleft end (BC) W₁ = P₁A₁(v₁Δt).
  • Work done by the fluid at the other end (DE)W₂ = P₂A₂(v₂Δt)
• Net work done on the fluid is W₁ – W₂ = (P₁A₁v₁Δt− P₂A₂v₂Δt)
• By the Equation of continuity Av=constant.
  • P₁A₁ v₁Δt – P₂A₂v₂Δt where A₁v₁Δt =P₁ΔV and A₂v₂Δt = P₂ΔV.
• Therefore Work done = (P₁− P₂) ΔVequation (a)
  • Part of this work goes in changing Kinetic energy, ΔK = (½)m (v₂² – v₁²) and part in gravitational potential energy,ΔU =mg (h₂ − h₁).
• The total change in energy ΔE= ΔK +ΔU = (½) m (v₂² – v₁²) + mg (h₂ − h₁). (i)
• Density of the fluid ρ =m/V or m=ρV

• Therefore in small interval of time Δt, small change in mass Δm
  • Δm=ρΔV (ii)
• Putting the value from equation (ii) to (i)

• ΔE = 1/2 ρΔV (v₂² – v₁²) + ρgΔV (h₂ − h₁)  equation(b)
• By using work-energy theorem: W = ΔE
  • From (a) and (b)
  • (P₁-P₂) ΔV =(1/2) ρΔV (v₂² – v₁²) + ρgΔV (h₂ − h₁)
  • P₁-P₂ = 1/2ρv₂² – 1/2ρv₁²+ρgh₂ -ρgh₁(By cancelling ΔV from both the sides).
• After rearranging we get,P₁ + (1/2) ρ v₁² + ρg h₁ = (1/2) ρ v₂² + ρg h₂
• P+(1/2) ρv²+ρg h = constant.
• This is the Bernoulli’s equation.

Bernoulli’s equation: Special Cases

1. When a fluid is at rest. This means v₁=v₂=0.

• From Bernoulli’s equation P₁ + (1/2) ρ v₁² + ρg h₁ = (1/2) ρ v₂² + ρg h₂
• By puttingv₁=v₂=0 in the above equation changes to
  • P₁-P₂= ρg(h₂-h₁). This equation is same as when the fluids are at rest.

2. When the pipe is horizontal.h₁=h₂.This means there is no Potential energy by the virtue of height.

• Therefore from Bernoulli’s equation(P₁ + (1/2) ρ v₁² + ρg h₁ = (1/2) ρ v₂² + ρg h₂)
• By simplifying,P+(1/2) ρ v² = constant.

Problem:-

Water flows through a horizontal pipeline of varying cross-section.If the pressure of waterequals 6cm of mercury at a point where the velocity of flow is 30cm/s, what is the pressure at the another point where the velocity of flow is 50m/s?

Answer:-

At R₁:- v₁ = 30cm/s =0.3m/s

P₁=ρg h=6×10^-2x13600x9.8=7997N/m²

At R₂:- v₂=50cm/s=0.5m/s

From Bernoulli’s equation: – P+ (1/2) ρ v²+ρg h=constant

P₁+ (1/2) ρ v₁² = P₂(1/2) ρ v₂²

7997+1/2x 1000x (0.3)² = P₂+1/2x 1000x (0.5)²

P₂=7917N/m²

=ρg h₂ = h₂x13600x9.8

h₂ = 5.9cmHg.

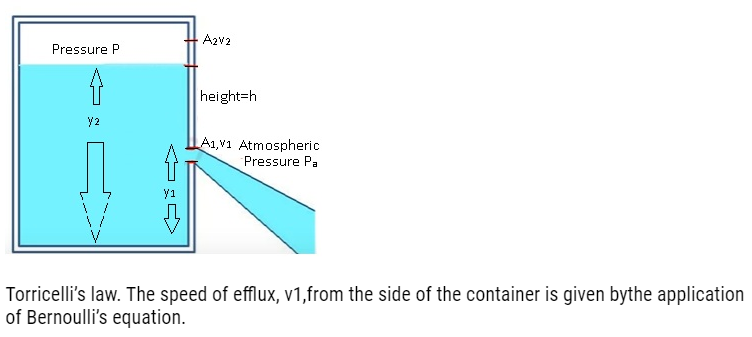
Torricelli’s law

• Torricelli law states that the speed of flow of fluid from an orifice is equal to the speed that it would attain if falling freely for a distance equal to the height of the free surface of the liquid above the orifice.
• Consider any vessel which has an orifice (slit)filled with some fluid.
• The fluid will start flowing through the slit and according to Torricelli law the speed with which the fluid will flow is equal to the speed with which a freely falling bodyattains such that the height from which the body falls is equal to the height of the slit from the free surface of the fluid.
• Let the distance between the free surface and the slit = h
• Velocity with which the fluid flows is equal to the velocity with which a freely falling body attains if it is falling from a height h.

Derivation of the Law:-

• Let A₁= area of the slit (it is very small), v₁= Velocity with which fluid is flowing out.
  • A₂=Area of the free surface of the fluid,v₂=velocity of the fluid at the free surface.
• From Equation of Continuity, Av=constant.Therefore A₁v₁ = A₂v₂.
  • From the figure, A₂>>>A₁, This implies v₂<<v₁(This meansfluid is at rest on the free surface), Therefore v₂~ 0.
• Using Bernoulli’s equation,
  • P+ (1/2) ρ v²+ρgh = constant.
• Applying Bernoulli’s equation at the slit:
  • P_a+(1/2) ρ v₁²+ρgy₁(Equation 1) where P_a=atmospheric pressure,y₁=height of the slit from the base.
• Applying Bernoulli’s equation at the surface:
• P+ρgy₂(Equation 2) where as v₂=0 therefore (1/2) ρ v₁²=0, y₂=height of the free surface from the base.
• By equating(1) and (2),
• P_a+ (1/2) ρ v₁²+ ρgy₁= P+ρgy₂
• (1/2) ρ v₁² = (P-P_a) + ρg(y₂-y₁)
• =(P-P_a) ρgh (where h=(y₂-y₁))
• v₁²=2/ρ [(P-P_a) + ρgh]
• Therefore v1=√2/ρ [(P-P_a) + ρgh].This is the velocity by which the fluid will come out of the small slit.
• v₁ is known as Speed of Efflux. This means the speed of the fluid outflow.

Case1:- The vessel is not closed it is open to atmosphere that means P=P_a.

• Therefore v₁=√2gh.This is the speed of a freely falling body.
• This is accordance to Torricelli’s law which states that the speed by which the fluid is flowing out of a small slit of a container is same as the velocity of a freely falling body.
• Case2:-Tank is not open to atmosphere but P>>P_a.
  • Therefore 2gh is ignored as it is very very large, hence v₁= √2P/ρ.
  • The velocity with which the fluid will come out of the container is determined by the Pressure at the free surface of the fluid alone.

Problem: –Calculate the velocity of emergence of a liquid from a hole in the side of a wide cell 15cm below the liquid surface?

Answer:-

By using Torricelli’slaw v1=√2gh

=√2×9.8x15x10^-2 m/s

=1.7m/s

Problem:- Torricelli’s barometer used mercury. Pascal duplicated it using French wine of density 984kgm^–3. Determine the height of the wine column for normal atmospheric pressure.

Answer:-

Density of mercury, ρ₁ = 13.6 × 10³kg/m³

Height of the mercury column, h₁ = 0.76 m

Density of French wine, ρ₂ = 984 kg/m³

Height of the French wine column = h₂

Acceleration due to gravity, g = 9.8 m/s²

The pressure in both the columns is equal, i.e.

Pressure in the mercury column= Pressure in the French wine column

ρ₁h₁g = ρ₂h₂g

h₂= ρ₁h₁/ ρ₂

= (13.6×10³x0.76)/984

= 10.5 m

Hence, the height of the French wine column for normal atmospheric pressure is 10.5 m.