Conservative & Non-Conservative Forces

• Conservative forces are those for which work done depends only on initial and final points.
  Example- Gravitational force, Electrostatic force.
• Non-Conservative forces are those where the work done or the kinetic energy did depend on other factors such as the velocity or the particular path taken by the object.
  Example- Frictional force.

The Conservation of Mechanical Energy

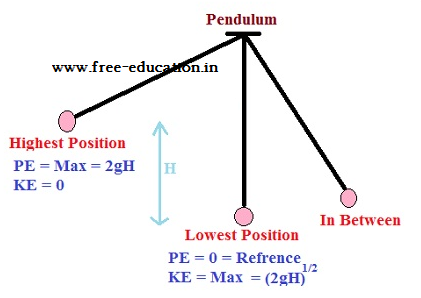
• Mechanical Energy is the energy associated with the motion and position of an object.
• The quantity K +V(x), is called the total mechanical energy of the system.
• For a conservative force, ΔK = ΔW = F(x) Δx
  Also, – V(x) = F(x) Δx
• This employs Δ(K+V) =0 for a conservative force.
• Individually the kinetic energy K and the potential energy V(x) may vary from point to point, but the sum is a constant.
• Conservative Force:
• A force F(x) is conservative if it can be derived from a scalar quantity V(x) by the relation  : F(x) = – dv/dx
• The work done by the conservative force depends only on the end points.
• A third definition states that the work done by this force in a closed path is zero.
• The total mechanical energy of a system is conserved if the forces, doing work on it, are conservative.

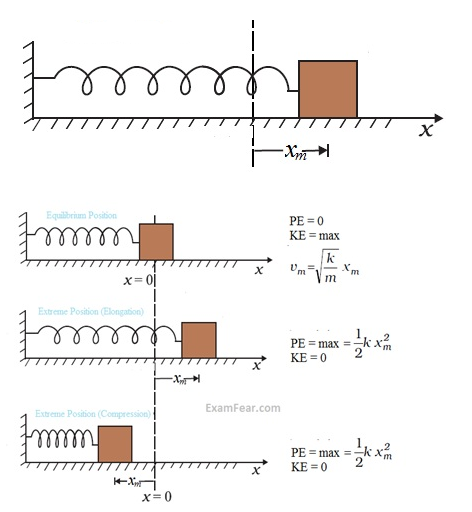
Potential energy of spring

• The spring force is an example of a variable force, which is conservative.
• In an ideal spring, F_s = − kx , this force law for the spring is called Hooke’s law.
• The constant k is called the spring constant. Its unit is N m^-1.
• The spring is said to be stiff if k is large and soft if k is small.

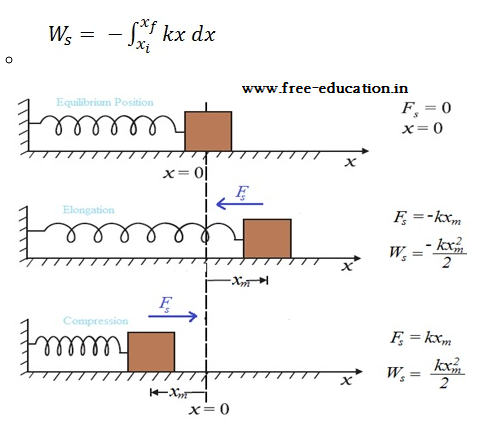
• Spring force is position dependent as first stated by Hooke, (F_s = − kx)
• Work done by spring force only depends on the initial and final positions. Thus, the spring force is a conservative force.
• We define the potential energy V(x) of the spring to be zero when block and spring system is in the equilibrium position.
• For an extension (or compression) x,  V(x) = kx²/2

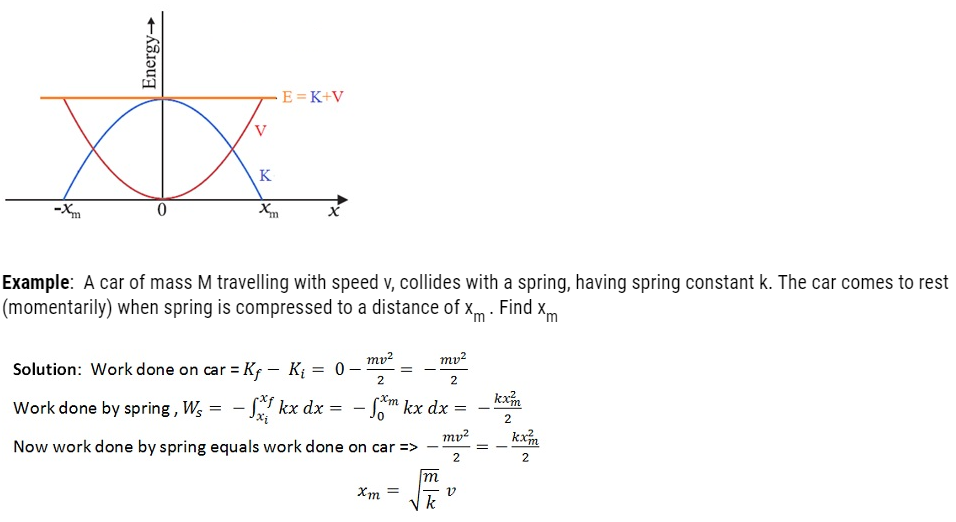
If the block of mass m is extended to x_m and released from rest, then its total mechanical energy at any arbitrary point x (where x lies between – x_m and + x_m) will be given by: