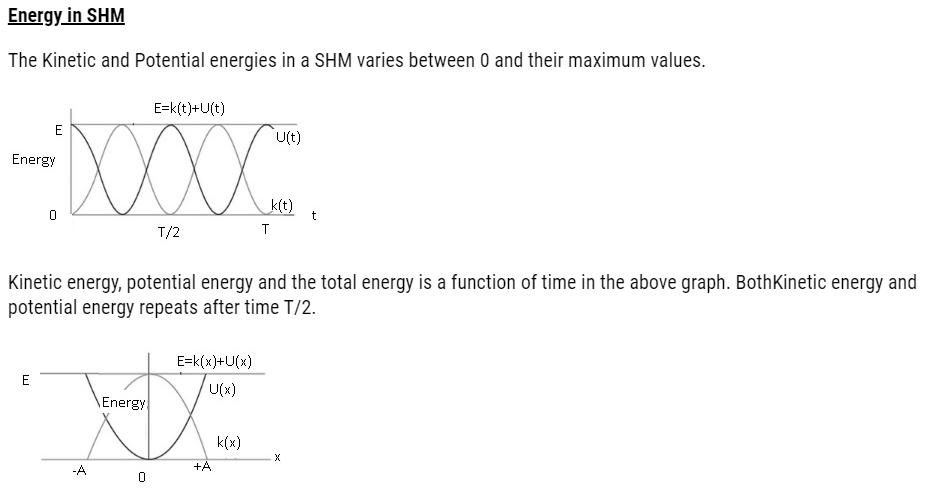
Kinetic energy, potential energy and the total energy is a function of displacement in the above graph.
The kinetic energy (K) of a particle executing SHM can be defined as
K= ½ mv2
= ½ mω2A2sin2 (ωt + φ)
K=½ k A2 sin2 (ωt + φ)
- The above expression is a periodic function of time, being zero when the displacement is maximum and maximum when the particle is at the mean position.
The potential energy (U) of a particleexecuting simple harmonic motion is,
U(x) = ½ kx2
U= ½ k A2 cos2 (ωt + φ)
- The potential energy of a particle executing simple harmonic motion is alsoperiodic, with period T/2, being zero at the mean position and maximum at the extremedisplacements.
Total energy of the system always remains the same
E = U + K
= ½ k A2 sin2 (ωt + φ) + ½ k A2 cos2 (ωt + φ)
E=½ k A2(sin2 (ωt + φ) + cos2 (ωt + φ))
The above expression can be written as
E = ½ k A2
Total energy is always constant.
Problem: –A block whose mass is 1 kgis fastened to a spring. The spring has a
spring constant of 50 N m–1. The block ispulled to a distance x = 10 cm from its equilibrium position at x = 0 on a frictionlesssurface from rest at t = 0. Calculate thekinetic, potential and total energies of theblock when it is 5 cm away from mean position?
Answer: -The block executes SHM, its angularfrequency, according to equation, ω= √k/m
= √ (50 N m–1)/ 1kg
= 7.07 rad s–1
Its displacement at any time t is then given by,
x (t) = 0.1 cos (7.07t)
Therefore, when the particle is 5 cm away fromthe mean position, we have
0.05 = 0.1 cos (7.07t)
Or cos (7.07t) = 0.5 and hence
sin (7.07t) = √3/2= 0.866
Then, the velocity of the block at x = 5 cm is
= 0.1 7.07 0.866 m s–1
= 0.61 m s–1
Hence the K.E. of the block,
=1/2 m v2
= [1kg (0.6123 m s–1 )2 ]
= 0.19 J
The P.E. of the block,
=1/2 kx2
= (50 N m–1 0.05 m 0.05 m)
= 0.0625 J
The total energy of the block at x = 5 cm,
= K.E. + P.E.
= 0.25 J
we also know thatmaximum displacement,K.E. is zero and hence the total energy of thesystem is equal to the P.E. Therefore, the totalenergy of the system,
= (50 N m–1 0.1 m 0.1 m)
= 0.25 J , which is same as the sum of the two energies ata displacement of 5 cm.This shows the result with the accordance of conservation of energy.

- T = 2√m/k where T is the period.
Problem: – A spring balance has a scale that reads from 0 to 50 kg. The length of the scale is 20 cm. A body suspended from this balance, when displaced and released, oscillates with a period of 0.6 s. What is the weight of the body?
Answer:
Maximum mass that the scale can read, M = 50 kg
Maximum displacement of the spring = Length of the scale, l = 20 cm = 0.2 m
Time period, T = 0.6 s
Maximum force exerted on the spring, F = Mg
where,g = acceleration due to gravity = 9.8 m/s2
F = 50 × 9.8 = 490 N
∴spring constant, k = F/l = 490/0.2 = 2450 N m-1.
Mass m, is suspended from the balance
∴Weight of the body = mg = 22.36 × 9.8 = 219.167 N
Hence, the weight of the body is about 219 N.
Problem: – A 5 kg collar is attached to a spring of spring constant 500 N m–1. It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by 10.0 cm and released. Calculate
(a) the period of oscillation,
(b) the maximum speed and
(c) maximum acceleration of the collar.
Answer:-
The period of oscillation as given by
T =2√m/k = 2 π√ (5.0 kg/500 Nm-1)
= (2π/10)s
= 0.63 s
(b) The velocity of the collar executing SHM is
given by,
v (t) = –Aω sin (ωt + φ)
The maximum speed is given by,
vm = Aω
= 0.1√ (k/m)
= 0.1√ (500Nm-1/5kg)
= 1 ms–1
and it occurs at x = 0
(c) The acceleration of the collar at thedisplacement x (t) from the equilibrium isgiven by,
a (t) = –ω2x (t)
= – k/m x (t)
Therefore the maximum acceleration is,
amax = ω2 A
= (500 N m–1/5kg) x0.1m
= 10 m s–2and it occurs at the extreme positions.