Ideal-gas Equation and Absolute Temperature

A thermometer that uses any gas, however, gives the same readings regardless of which gas is used because all gases have same expansion at low temperature.

Variables that describe the behaviour of gas are:-

• Quantity(mass)
• Pressure
• Volume
• Temperature i.e. (P,V,T) where (T = t + 273.15; t is the temperature in °C)

Gases which have low density obey certain laws: –

1.Boyle’s Law– PV = constant(when temperature T is constant)

2.Charles’ Law– V/T = constant (when pressure P is constant)

Problem:The triple points of neon and carbon dioxide are 24.57 K and 216.55 K respectively. Express these temperatures on the Celsius and Fahrenheit scales?

Solution: Celsius and Fahrenheit scales are related as

T_F = (9/5)T_C + 32   … (ii)

For neon:

 = 24.57 K

 = 24.57 – 273.15 = –248.58°C

T_F = (9/5) T_C + 32

 =9/5(-248.58) +32

=415.44 ^oF

For carbon dioxide:

 = 216.55 K

= 216.55 – 273.15 = –56.60°C

T_F = (9/5)T_C + 32

     =9/5(-56.60) +32

      = -69.88 ^oC

Problem:Two absolute scales A and B have triple points of water defined to be 200 A and 350 B. What is the relation between T_A and T_B?

Solution:

Triple point of water on absolute scale A, T₁ = 200 A

Triple point of water on absolute scale B, T₂ = 350 B

Triple point of water on Kelvin scale, T_k= 273.15 K

The temperature 273.15 K on Kelvin scale is equivalent to 200 A on absolute scale A.

T₁ = T_k

200 A = 273.15 K

 Therefore,

A =   273.15/200

The temperature 273.15 K on Kelvin scale is equivalent to 350 B on absolute scale B.

T₂ = T_k

350 B = 273.15

B=  273.15/350

T_A is triple point of water on scale A. T_B is triple point of water on scale B

Therefore,

Thermal Expansion

• Thermal expansion is the phenomenon of increase in dimensions of a body due to increase in its temperature.

Examples of Thermal Expansion

• The water is cold at the top of the lake because it expands and becomes less dense. So when this water freezes it insulates the water below it from the outside which means cold air is like a blanket. It is because of this property many fish can survive in the winter.

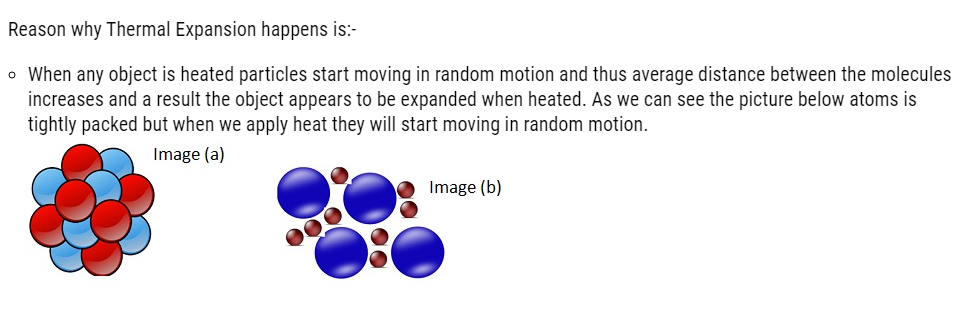
As we can see in the Image (a) molecules are very tightly packed but when heated the molecules start moving apart in random motion, which can be seen in Image (b).

• When an object is cooled it contracts which is referred as negative thermal expansion.

Types of Thermal Expansion

1. Linear Expansion :- The expansion in length
2. Area Expansion :- The expansion in area
3. Volume Expansion :- The expansion in volume

Linear Expansion

Linear Expansion means expansion in length due to increase in temperature. Linear expansion means fractional change in length i.e. how the length is changing with respect to original length.

• It is denoted by α_a
• It is characteristic of the substance and it varies with temperature.

Coefficient of Volume can be defined as degree of volume expansion divided by change in temperature.

• It is denoted by α_v.
• It is characteristic of the substance
• It varies with temperature.

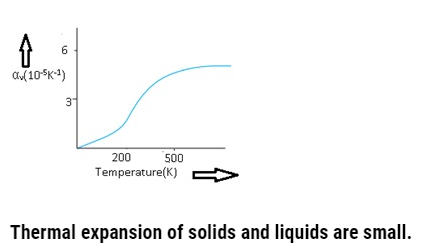
If graph is plotted between α_v and temperature,then initially α_v is a changing linearly then it varies non-linearly and at higher temperatures and then it becomes constant.

Coefficient of volume expansion of copper as a function of temperature-