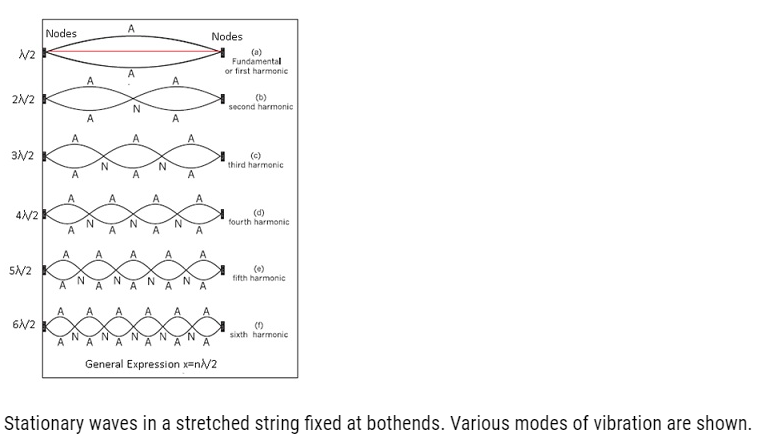
Modes of Oscillations:-
- ν= (vn)/2L where v=speed of the travelling wave, L=length of the string, n=any natural number.
- First Harmonic:-
- For n=1, mode of oscillation is known as Fundamental mode.
- Therefore ν1=v/(2L).This is the lowest possible value of frequency.
- Therefore ν1is the lowest possible mode of the frequency.
- 2 nodes at the ends and 1 antinode.
- Second Harmonic:-
- For n=2, ν2=(2v)/ (2L) =v/L
- This is second harmonic mode of oscillation.
- 3 nodes at the ends and 2 antinodes.
- Third Harmonic:-
- For n=3,ν3 = (3v)/ (2L).
- This is third harmonic mode of oscillation.
- 4 nodes and 3 antinodes.
Problem:- Find the frequency of note emitted (fundamental note) by a string 1m long and stretched by a load of 20 kg, if this string weighs 4.9 g. Given, g = 980 cm s–2?
Answer:-
L = 100 cm T = 20 kg = 20 × 1000 × 980 dyne
m= 4.9/100 = 0.049 g cm-1
Now the frequency of fundamental note produced,
ν= (1/2L) √ (T/m)
ν = 1/ (2×100) √(20x1000x980)/(0.049)
=100Hz
Problem:- A pipe 20 cm long is closed at one end, which harmonic mode of the pipeis resonantly excited by a 430 Hzsource? Will this same source can bein resonance with the pipe, if both ends are open? Speed of sound = 340ms–1?
Answer:-
The frequency of nth mode of vibration of a pipe closed at one endis given by
νn=(2n 1)ν/4L
ν=340ms-1; L=20cm=0.2m;νn=430Hz.
Therefore 430= ((2n-1) x 340)/ (4×0.2)
=>n=1
Therefore, first mode of vibration of the pipe is excited, for open pipe sincen must be an integer, the same source cannot be in resonance with thepipe with both ends open.
Nodes and Antinodes: system closed at one end
- For a system which is closed at one end,only one node is formed at the closed end.
- Consider there is one fixed end(x=0) and one open end(x=L), and a string is attached between these two ends.
- At x=L, antinodes will be formed.This means amplitude will be maximum at this end.
- Condition for formation of antinodes is x= (n+ (1/2)) (λ/2).=>L=(n+ (1/2)) (λ/2)
- =>λ=(2L)/(n+(1/2)).This expression shows that the values of wavelength is restricted. n=0, 1, 2, 3…
- Corresponding frequencies will be ν= v/(2L)(n+1/2) (By using ν=v/λ);n=0,1,2,3, …
Modes of oscillations:-
- Fundamental frequency:- Also known as First Harmonic:-It corresponds to lowest possible value for n. That is n=0.
- The expression for fundamental frequency is ν0 = v/(2L)x1/2 = v/(4L)
- Odd Harmonics
- n=1 ; ν =v/(2L)(1+(1/2)) = (3v)/(4L) =3ν0
- n=2; ν =v/(2L)(2+(1/2))= (5v)/(4L)=5ν0
- n=3;ν =v/(2L)(3+(1/2))=(7v)/(4L)=7ν0
- For a system which is closed at one end and open at another end will get one fundamental frequency and all other odd harmonics.


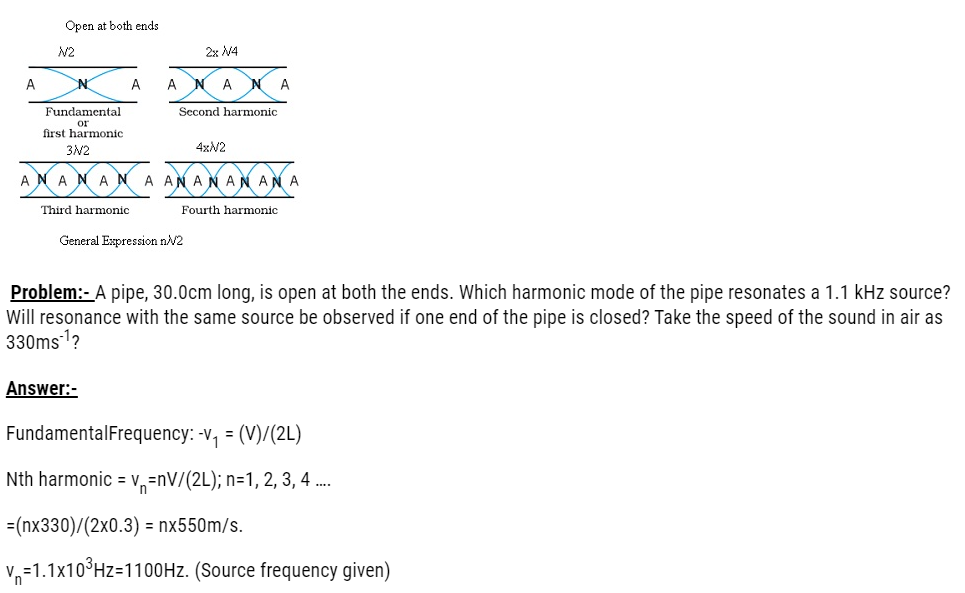
Therefore nx550=1100 => n=2. It is the second harmonic.
- Fundamental Frequency: – ν1= (V)/ (4L)
Odd harmonics :- (3V)/ (4L), (5V)/ (4L), (7V)/ (4L) ….
=>ν1=νY =275Hz. Where νY = Fundamental Frequency
=>nν1 = 1100 => n=1100/275=4
This should correspond to 4th harmonic but 4th harmonic cannot be present as only odd harmonics are present.
Therefore the same source cannot be resonated if the pipe is closed at one end.