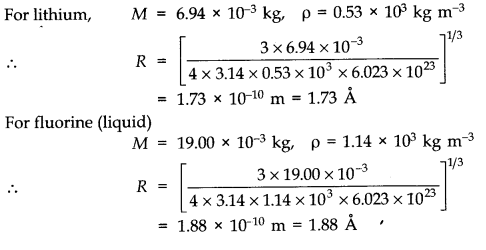NCERT Solutions for Class 11 Physics Chapter 13 Kinetic Theory
QUESTIONS FROM TEXTBOOK ( Kinetic Theory Notes )
Question 13. 1. Estimate the fraction of molecular volume to the actual volume occupied by oxygen gas at STP.’ Take the diameter of an oxygen molecule to be 3 A.
Answer: Diameter of an oxygen molecule, d = 3 A = 3 x 10-10 m. Consider one mole of oxygen gas at STP, which contain total NA = 6.023 x 1023 molecules


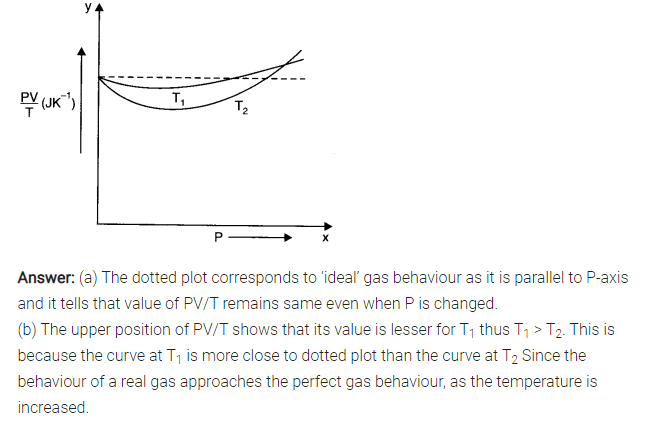
Question 13. 3. Following figure shows plot of PV/T versus P for 1.00 x 10-3 kg of oxygen gas at two different temperatures.
(a) What does the dotted plot signify?
(b) Which is true : T1> T2 or T1< T2?
(c) What is the value of PV/T where the curves meet on the y-axis?
(d) If we obtained similar plots for 1.00 x 10-3 kg of hydrogen, would we get the same value of PV/T at the point where the curves meet on the y-axis? If not, what mass of hydrogen yields the same value of PV/T (for the low-pressure high-temperature region of the plot) ? (Molecular mass of H2 = 2.02 u, of O2 = 32.0 u, R = 8.31 J mol-1 K-1.)

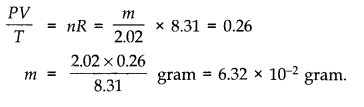
Question 13. 4. An oxygen cylinder of volume 30 Hire has an initial gauge pressure of 15 atmosphere and a temperature of 27 °C. After some oxygen is withdrawn from the cylinder, the gauge pressure drops to 11 atmosphere and its temperature drops to 17 °C. Estimate the mass of oxygen taken out of the cylinder. (R = 8.31 J mol-1 K-1, molecular mass of O2 = 32 u.)

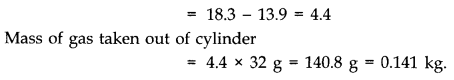







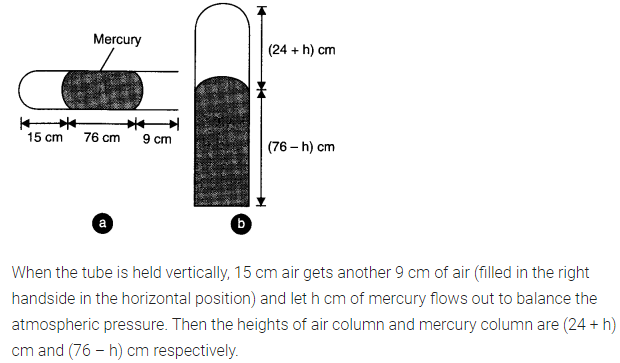
Question 13. 11. A meter long narrow bore held horizontally (and closed at one end) contains a 76 cm long mercury thread which traps a 15 cm column of air. What happens if the tube is held vertically with the open end at the bottom?
Answer: When the tube is held horizontally, the mercury thread of length 76 cm traps a length of air = 15 cm. A length of 9 cm of the tube will be left at the open end. The pressure of air enclosed in tube will be atmospheric pressure. Let area of cross-section of the tube be 1 sq. cm.
.’. P1 = 76 cm and V1 = 15 cm3


Question 13. 13. A gas in equilibrium has uniform density and pressure throughout its volume. This is strictly true only if there are no external influences. A gas column under gravity, for example, does not have uniform density (and pressure). As you might expect, its density decreases with height. The precise dependence is given by the so-called law of atmospheres n2 = n1 exp [ – mg (h2 – h1)/kBT]
where n2, n1 refer to number density at heights h2 and h1 respectively. Use this relation to derive the equation for sedimentation equilibrium of a suspension in a liquid column :
n2 = n1 exp [ – mg NA(ρ – P) (h2 – h1 )/(ρ RT)] where ρ is the density of the suspended particle, and ρ that of surrounding medium. [NA is Avogadro’s number, and R the universal gas constant.]
[Hint: Use Archimedes principle to find the apparent weight of the suspended particle.]
Answer: Considering the particles and molecules to be spherical, the weight of the particle is