The principle of superposition of waves
- Principle of superposition of waves describes how the individual waveforms can be algebraically added to determine the net waveform.
- Waveform tells about the overall motion of the wave.It does not tell about individual particles of the wave.
- Suppose we have 2 waves and
- Example of superposition of waves is Reflection of waves.
- Mathematically: –
Case1:-
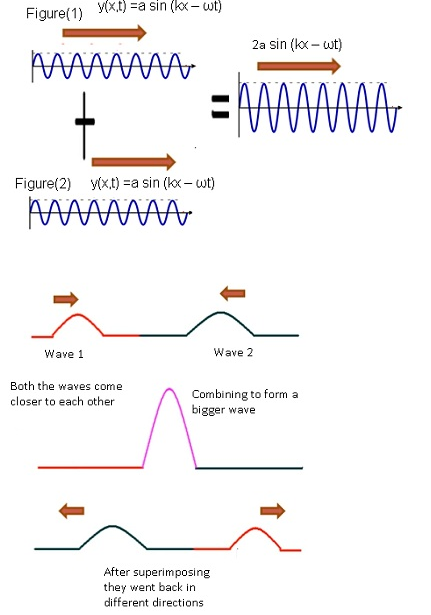
- Consider 2waves which are in phase with each other. They have the same amplitude, same angular frequency, and same angular wave number.
- If wave 1 is represented by y1(x, t) =a sin (kx – ωt).
- Wave 2 is also represented by y2(x, t) =a sin (kx – ωt).
- By the principle of superposition the resultant wave (2a sin (kx – ωt)) will also be in phase with both the individual waves but the amplitude of the resultant wave will be more.
Case2:-
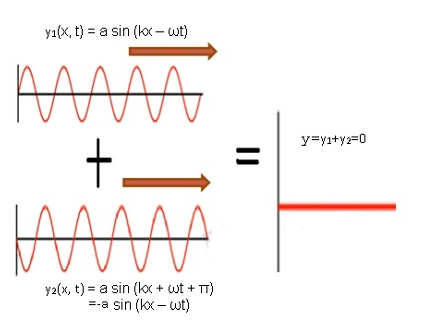
- Consider when the two waves are completely out of phase.i.e. φ = π
- If wave 1 is represented by y1(x, t) =a sin (kx – ωt).
- Wave 2 is represented by y2(x, t) =a sin (kx – ωt+ π).
- =>y2=asin(π-(-kx+ ωt) =>y2=-a sin(kx- ωt)
- Therefore by superposition principle y=y1+y2=0
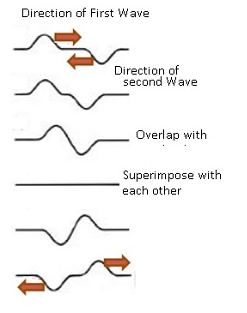


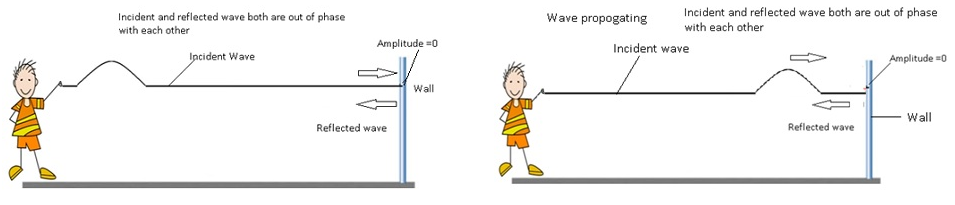
Reflection at rigid boundary
- Consider a string which is fixed to the wall at one end. When an incident wave hits a wall,it will exerta force on the wall.
- By Newton’s third law, the wall exerts an equal and opposite force of equal magnitude on the string.
- Since the wall is rigid wall won’t move, therefore no wave is generated at the boundary.This implies the amplitude at the boundary is 0.
- As both the reflected wave and incident wave are completely out of phase at the boundary.Therefore φ=π.
- Therefore, yi(x, t) = a sin (kx – ωt),
- yr(x, t) = a sin (kx + ωt + π) = – a sin (kx + ωt)
- By superposition principle y= yi + yr =0
- Conclusion: –
- The reflection at the rigid body will take place with a phase reversal of π or 180.

Standing (Stationary) Waves
- A stationary wave is a wave which is not moving,i.e. it is at rest.
- When two waves with the same frequency,wavelengthand amplitude travelling in opposite directions will interfere they produce a standing wave.

- Explanation:-
- Consider Ist wave in the figure and suppose we have a rigid wall which does not move. When anincident wave hits the rigid wall it reflects back with a phase difference of π.
- Consider IInd wave in the figure, when the reflected wave travels towards the left there is another incident wave which is coming towards right.
- The incident wave is continuously coming come from left to right and the reflected wave will keep continuing from right to left.
- At some instant of time there will be two waves one going towards right and one going towards left as a result these two waves will overlap and form a standing wave.
- Mathematically:
- Wave travelling towards left yl(x,t) =a sin(kx– ωt) and towards right yr(x,t) =a sin (kx + ωt)
- The principle of superposition gives, for the combined wave
- y (x, t) = yl(x, t) + yr(x, t)= a sin (kx – ωt) + a sin (kx + ωt)
- y(x,t)= (2a sin kx) cos ωt (By calculating and simplifying)
- The above equation represents the standing wave expression.
- Amplitude = 2a sin kx.
- The amplitude is dependent on the position of the particle.
- The cos ωt represents the time dependent variation or the phase of the standing wave.
Difference between the travelling wave and stationary wave
| Travelling Wave(Progressive Wave) | Stationary Wave (Standing wave) |
| Waveform moves. Movement of the waveform is always indicated by the movement of the peaks of the wave. | Waveform doesn’t move.Peaks don’t move. |
| Wave amplitude is same for all the elements in the medium. Denoted by ‘A’. | Wave amplitude is different for different elements.Denoted by asinkx. |
| Amplitude is not dependent on the position of the elements of the medium. | Amplitude is dependent on the position of the elements of the medium. |
| y(x,t)=asin(kx– ωt + φ ) | y(x,t)=2asin(kx)cos(ωt) |