Torque & Angular Momentum

• The rotational analogue of force is moment of force (Torque).
• If a force acts on a single particle at a point P whose position with respect to the origin O is given by the position vector r the moment of the force acting on the particle with respect to the origin O is defined as the vector product t = r × F =  rF sinΘ

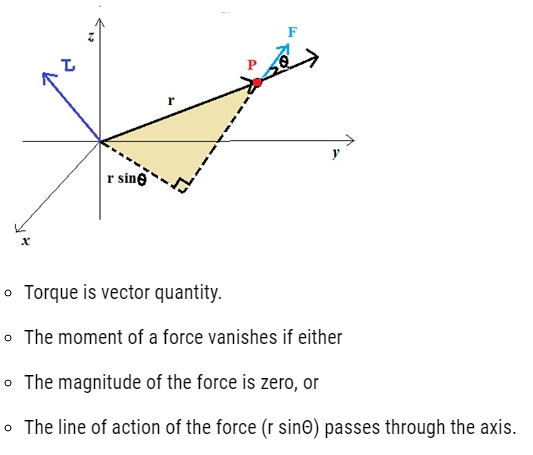
• The quantity angular momentum is the rotational analogue of linear momentum.
• It could also be referred to as moment of (linear) momentum.
• l = r × p
• Rotational analogue of Newton’s second law for the translational motion of a single particle:  dl/st = τ

Torque and angular momentum of system of particles:

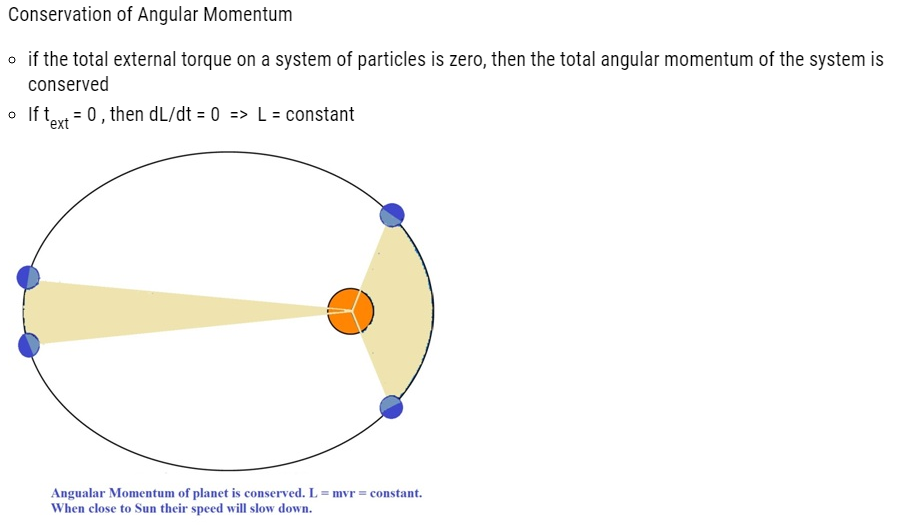
Equilibrium of Rigid Body

• A force changes the translational state of the motion of the rigid body, i.e. it changes its total linear momentum.
• A torque changes the rotational state of motion of the rigid body, i.e. it changes the total angular momentum of the body

Note: Unless stated otherwise, we shall deal with only external forces and torques.

• A rigid body is said to be in mechanical equilibrium, if both its linear momentum and angular momentum are not changing with time. This means
• Total force should be zero => Translational Equilibrium
• Total torque should be zero => Rotational Equilibrium

• When you open the lid of a jar , you apply couple on it

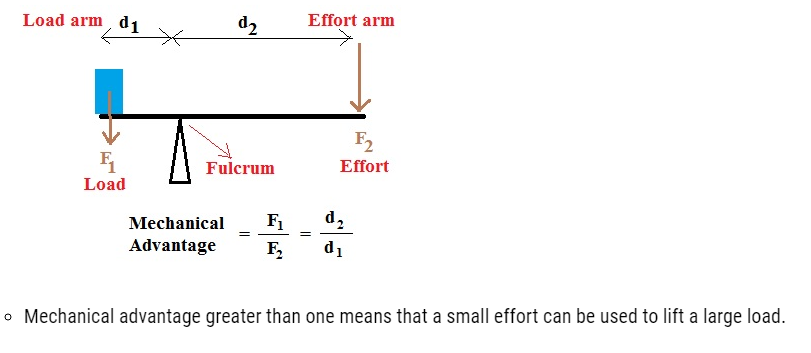
• An ideal lever is essentially a light rod pivoted at a point along its length. This point is called the fulcrum
• The lever is a system in mechanical equilibrium.