Avogadro Law

• It states that equal volumes of all gases under the same conditions of temperature and pressure
  contain equal number of molecules. Mathematically,

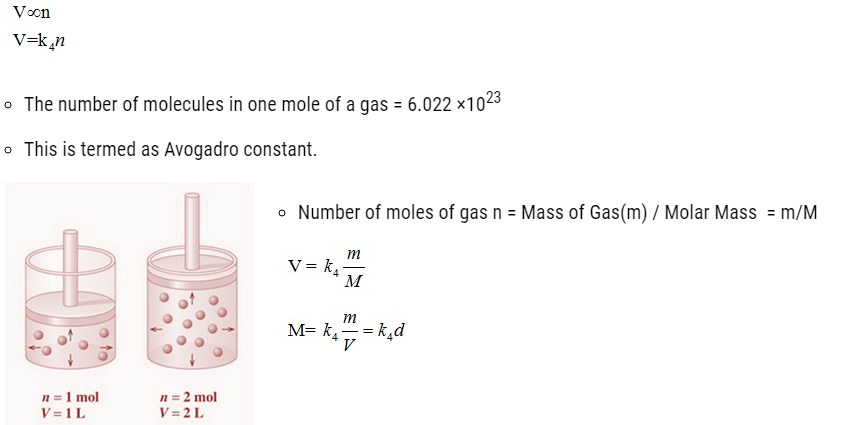
Ideal Gas Equation

• The gases following Boyle’s law, Charles’law and Avogadro law firmly are termed as anideal gas.
• From Boyle’s law we have  V ∝ 1/p (Constant T, n)
• From Charles’ law we have  V ∝ T (Constant p, n)
• From Avogadro’s law we have V ∝ n (Constant T, n)
• Combining them we get,  V ∝ nT/p
• or V = nRT/p 

pV = nRT ………………………… (IDEAL GAS EQUATION)

R =pV/nT

R= Gas Constant. It is same for all gases.

Problem:

Using the equation of state pV = nRT; show that at a given temperature density of a gas is proportional to gas pressure.

Solution:

Using Ideal gas equation, pV = nRT ……….. (1)

p → Pressure of gas

V → Volume of gas

n→ Number of moles of gas

R → Gas constant

T → Temperature of gas

From equation (1),

p = n RT/V

n = Mass of Gas (m) /Molar Mass of gas (M)

Putting value of n in the equation, we have

 p = m RT/ MV ————(2)

Density (ρ) = m /V —————-(3)

Putting (3) in (2) we get

p = ρ RT / M

Or ρ = PM / RT

Problem:

Calculate the total pressure in a mixture of 8 g of dioxygen and 4 g of dihydrogen confined in a vessel of 1 dm³ at 27°C. R = 0.083 bar dm3 K^–1 mol^–1.

Solution:

m (Oxygen) = 8 g,

M (Oxygen) = 32 g/mol

m ( Hydrogen) = 4 g,

M (Hydrogen) = 2 g/mol

n (Amount of oxygen) = 8/ 32 = 0.25 mol

n (Amount of hydrogen) = 4/2 = 2 mol

According to ideal gas equation,  

PV = n RT,

 P X 1 = (0.25 + 2) X 0.083 X 300 = 56.02 bar

Total pressure of the mixture is 56.02 bars.

Problem:

Calculate the volume occupied by 8.8 g of CO2 at 31.1°C and 1 bar pressure. R = 0.083 bar L K–1 mol^-1.

Solution:

According to ideal gas equation, PV = nRT

But n = Mass of Gas (m)/ Molar mass of Gas (M)

PV = (m/M) RT

For CO₂ , M = 44 g/mol

Putting the values

1 x V = (8.8 / 44) x 0.083 x 304.1

 = 5.05 L

Volume occupied is 5.05 L.

Density and Molar Mass of a Gaseous Substance

• As per ideal gas equation,

pV = nRT

Or n/V = p/RT

• As we know n = Mass of Gas (m) / Molar Mass of Gas (M) = m/M

So, m/MV = p/RT

d/M= p/RT

• Or Molar mass = M = dRT/p

Problem:

At 0°C, the density of a certain oxide of a gas at 2 bar is same as that of dinitrogen at 5 bar. What is the molecular mass of the oxide?

Solution:

Using the formula  ρ = Mp/RT

or p = ρ RT/ M

According to the question,

For certain oxide gas

2 = ρ RT/ M ……………(1)

For nitrogen

5 = ρ RT/28 ………………….(2)

From equation (1) & (2), we get

5/2 = M/28

Or

M = 5 X 28/ 2 = 70g/mol

Problem:

Density of a gas is found to be 5.46 g/dm3 at 27 °C at 2 bar pressure. What will be its density at STP?

Solution:

According to the ideal gas

Density ρ = p x M/ RT

According to the question,

5.46 = 2 x M/ 300 x R    ……… (1)

ρ_STP = 1 x M/ 273 x R    ……….. (2)

From equation (1) & (2),

ρ_{STP =}  (1 x M/ 273 x R)   x (300 x R/ 2 x M) = 300 / 273 X 2 = 3.00 g/dm³

Density of the gas at STP will be 3 g dm^–3.

Problem:

Calculate the total number of electrons present in 1.4 g of dinitrogen gas.

Solution:

m ( Nitrogen) = 1.4 g

M (Nitrogen) = 28 g mol^–1

n (Amount of nitrogen) = 1.4 / 28 = 0.05 mol

Hence number of nitrogen molecule in 0.05 mol = 6.023 x 10²³  x 0.05 = 3.0115 x 10²²

Number of electrons in one molecule of nitrogen = 14