- Many properties of matter such as length, area, volume, etc., are quantitative in nature.
- Any quantitative observation or measurement is represented by a number followed by units in which it is measured.
- For example: – length of a room can be represented as 6 m; here 6 is the number and m denotes metre – the unit in which the length is measured.
Two different systems of measurement are as follows:-
- English System
- Metric System

The metric system which originated in France in late eighteenth century was more convenient as it was based on the decimal system.
The International System of Units (SI)
The International system of Units (in French Le System International d’Unites-abbreviated as SI) was established by 11th General Conference on Weights and Measures (CGPM from Conference General des Poids at Measures).
- The SI system has seven base units and they are listed in figure below. These units pertain to the seven fundamental scientific quantities.
- The other physical quantities such as speed, volume, density etc. can be derived from these quantities.


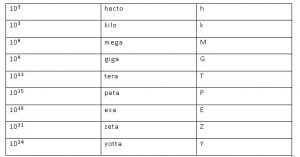
Prefixes used in SI System

Mass and Weight — Mass of a substance is the amount of matter present in it while weight is the force exerted by gravity on an object. The mass of a substance is constant whereas its weight may vary from one place to another due to changes in gravity. The mass of a substance can be determined very accurately by using an analytical balance.
or
- Mass is defined as the amount of matter present in a substance.
- Weight is defined as the force exerted by the gravity on an object.
- The mass of a substance is constant whereas its weight may vary from one place to another due to change in gravity.
- The mass of a substance can be determined very accurately in the laboratory by using an analytical balance.
- The SI unit of mass is kilogram.

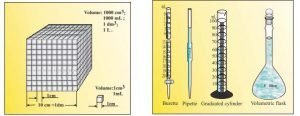
Volume — Volume has units of (length)3. So volume has units of m3 or cm3 or dm3 . A common unit, litre (L) is not an SI unit, is used for measurement of volume of liquids. 1 L = 1000 mL, 1000 cm3 = 1 dm3
or
- Volume has the units of (length) 3. So in SI system, volume has units of m3.
- A common unit, litre (L) which is not an SI unit, is used for measurement of volume of liquids.
- 1 L = 1000 mL, 1000 cm3 = 1 dm3.
- In the laboratory, volume of liquids or solutions can be measured by graduated cylinder, burette, pipette etc.
Density — Density of substance is its amount of mass per unit volume. SI unit of density = Si unit of mass / SI unit of volume = kg/m3 . This unit is quite large and a chemist often expresses density in g cm-3 .
Temperature — There are three common scales to measure temperature – .C (degree celsius), .F (degree Fahrenheit) and K (kelvin). Here, K is the SI unit.
F = 9/5(C) + 32
K = C + 273.15
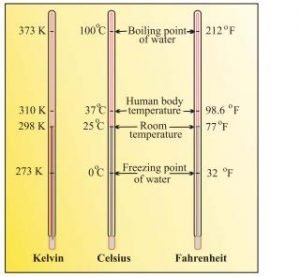
Note — Temperature below 0 ºC (i.e. negative values) are possible in Celsius scale but in Kelvin scale, negative temperature is not possible.
Scientific Notation —
In which any number can be represented in the form N x 10 n (Where n is an exponent having positive or negative values and N can vary between 1 to 10)
e.g. We can write 232.508 as 2.32508 x 102 in scientific notation. Similarly, 0.00016 can be written as 1.6 x 10-4
Uncertainty in measurement
- Since the chemistry is the study of atoms and molecules which have extremely low masses and are present in extremely large numbers, a chemist has to deal with numbers as large as 602,200,000,000,000,000,000,000 for the molecules of 2 g of hydrogen gas or as small as 0.00000000000000000000000166 g mass of a H atom.
- This problem is solved by using scientific notation for such numbers, i.e., exponential notation in which any number can be represented in the form N × 10n where n is an exponent having positive or negative values and N can vary between 1 to 10.
Problem:-
Convert the following into basic units:
(i) 28.7 pm
(ii) 15.15 pm
(iii) 25365 mg
Answer:-
(i) 28.7 pm:
1 pm = 10–12 m
28.7 pm = 28.7 × 10–12 m
= 2.87 × 10–11 m
(ii) 15.15 pm:
1 pm = 10–12 m
15.15 pm = 15.15 × 10–12 m
= 1.515 × 10–12 m
(iii) 25365 mg:
1 mg = 10–3 g
25365 mg = 2.5365 × 104 × 10–3 g
Since,
1 g = 10–3 kg
2.5365 × 101 g = 2.5365 × 10–1 × 10–3 kg
25365 mg = 2.5365 × 10–2 kg
Problem:-
If the speed of light is 3.0 ×108 m s-1, calculate the distance covered by light in 2.00 ns.
Answer:-
According to the question:
Time taken to cover the distance = 2.00 ns
= 2.00 × 10–9 s
Speed of light = 3.0 × 108 ms–1
Distance travelled by light in 2.00 ns
= Speed of light × Time taken
= (3.0 × 108 ms–1) (2.00 × 10–9 s)
= 6.00 × 10–1 m
= 0.600 m
Question 15. [NCERT Excersice]
Match the following prefixes with their multiplies
Prefixes Multiples
(i) micro 106
(ii) deca 109
(iii) mega 10-6
(iv) giga 10-15
(v) femto 10
Solution.
(i) micro → 10-6
(ii) deca → 10
(iii) mega → 106
(iv) giga → 109
(v) femto → 10-15
Question 18. [NCERT Excersice]
Express the following in the scientific notation:
(i) 0.0048
(ii) 234,000
(iii) 8008
(iv) 500.0
(v) 6.0012
Solution.
(i) 4.8 x 106
(ii) 2.34 x 105
(iii) 8.008 x 103
(iv) 5.00 x 102
(v) 6.0012 x 100 or 6.0012
Question 22. [NCERT Excercise]
If the speed of light is 3.0 x 108 m s-1, calculate the distance covered by light in 2.00 ns.
Solution.
Speed of light = 3.0 x 108 m s-1
Distance covered by light in 2.00 ns = 3.0 x 108 x 2 x 10-9 = 6.00 x 10-1 m = 0.600 m
Question 27. [NCERT Excersice]
Convert the following into basic units :
(i) 28.7 pm
(ii) 15.15pm
(iii) 25365 mg
Q. What is the S.I. unit of Density?
Ans. Kg/m3
Q. What is the relation between temperature in degree celsius and degree fahrenheit?
Ans. F = 9/5 (C) + 32

Q. Express the following in the scientific notation with 2 significant figures-
(a) 0.0048 (b) 234000 (c) 200.0
Ans. (a) 4.8 x 10-3 (b) 2.3 x 105 (c) 2.0 x 102
Q. What is the difference between 160 cm and 160.0 cm.
Ans. 160 has three significant figures while 160.0 has four significant figures. Hence, 160.0 represents greater accuracy.